Answer:
a) Third Quadrant
b) 7π/4 --> Option (4)
c) --> Option (1)
d) 1 --> Option (1)
e) --> Option (2)
f) - --> Option (2)
g) --> Option (1)
h) --> Option(2)
Step-by-step explanation:
Ok, lets properly define some technical term here.
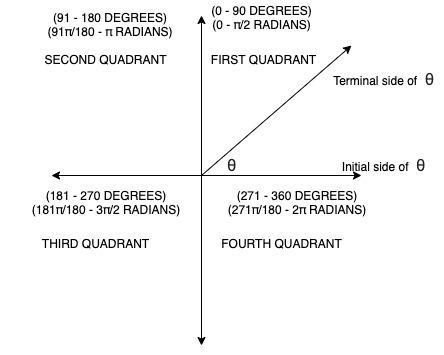
The terminal side of an angle is the side of the line after that it has made a turn (angle). I will drive my point home with the attachment to this solution
The initial side of an angle is the side of the line before the line made a turn(angle)
a) 1 complete revolution = = 2π rads
we can convert the radians to degrees using the above conversion rate
=> will be:
solving the expression above, 420π/2π =
From the value of the angle in degree and having in mind that
b) Co-terminal angles are angles which share the same initial and terminal side
To find the co-terminal of an angle we add or subtract 360 to the value if in degrees or 2π if in radians. From the value we want to find its co-terminal, because of the presence of π, its value is in radians and as such we add or subtract 2π from the value. If we perform subtraction, the negative co-terminal of the angle has been evaluated and the positive co-terminal is evaluated if we perform addition.
So, to get the positive co-terminal of -π/4, we add 2π and doing that, we get:
2π - π/4 = 7π/4
c) The value of sin(π/3) * cos(π) is ?
Applying special angle properties: (More on the special angle in the diagram attached to this solution)
sin(π/3) =
cos(π) = -1
substituting the values above into the expression, we have:
d) if , f(π/4) = ?
In trignometry,
Applying special angle properties again,
sin(π/4) =
cos(π/4) =
The expression becomes . Simplifying, we get:
2/4 + 2/4 = 1/2 + 1/2 = 1
e) cos(3π/4)
3π/4 is not an acute angle(angle < less than π/2 rad) and as such, we need to get its related acute angle. Now 3π/4 rads is in the second quadrant, this means that we will have to subtract 3π/4 from π to get the related acute angle.
π - 3π/4 = π/4
so instead of working with 3π/4, we work with its related acute angle which is π/4
cos(3π/4) is equivalent to cos(π/4) = (special angle properties)
f) sin(11π/6)
11π/6 is not an acute angle(angle less than π/2 rad) and it is in the fourth quadrant. This means that to get its related acute angle, we have to subtract it from 2π
2π - 11π/6 = π/6
sin(11π/6) is equivalent to -sin(π/6) = -1/2 (special angle properties).
Note that there is a minus in the answer. That had nothing to do with the special angle properties but rather, the fact that:
- At the fourth quadrant, only the cosine trignometric ratio is positive
- At the first quadrant, all trignometric ratios are positive
- At the second quadrant, only the sine trignometric ratio is positive
- At the third quadrant, only the tangent trignometric ratio is positive
g) sin(π/6) + tan(π/4)
using special angle properties:
sin(π/6) = 1/2 and tan(π/4) = 1
the expression simplifies to: 1/2+1 = 3/2
h) cos(4π/3)
4π/3 is not an acute angle and it is in the third quadrant
To get its related acute angle, we have to subtract it from 3π/2
3π/2 - 4π/3 = π/6
so, cos(4π/3) = -cos(π/6) (The negative value is because of the fact that at the third quadrant, only the tangent trignometric ratio is positive)
using special angle properties, -cos(π/6) =