Explanation:
A Riemann Sum is the sum of areas under a curve. It approximates an integral. There are various ways the area under a curve can be approximated, and the different ways give rise to different descriptions of the sum.
A Riemann Sum is often specified in terms of the overall interval of "integration," the number of divisions of that interval to use, and the method of combining function values.
<u>Example Problem</u>
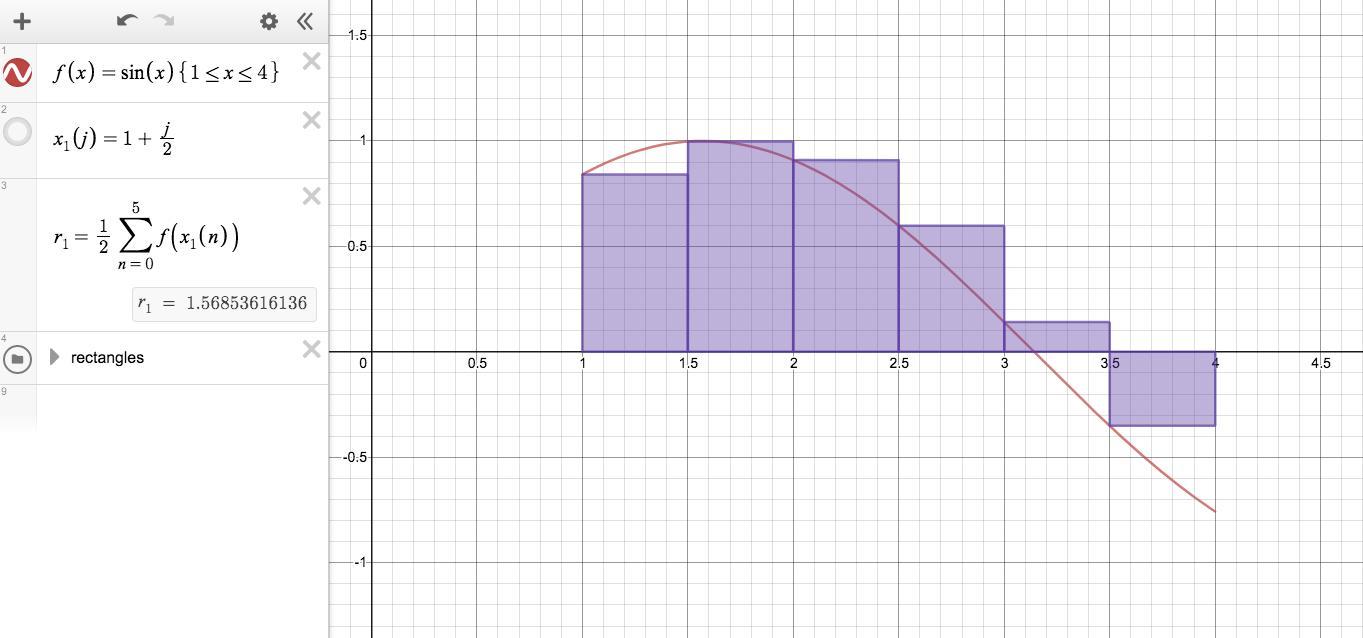
For the example attached, we are finding the area under the sine curve on the interval [1, 4] using 6 subintervals. We are using a rectangle whose height matches the function at the left side of the rectangle. We say this is a <em>left sum</em>.
When rectangles are used, other choices often seen are <em>right sum</em>, or <em>midpoint sum</em> (where the midpoint of the rectangle matches the function value at that point).
Each term of the sum is the area of the rectangle. That is the product of the rectangle's height and its width. We have chosen the width of the rectangle (the "subinterval") to be 1/6 of the width of the interval [1, 4], so each rectangle is (4-1)/6 = 1/2 unit wide.
The height of each rectangle is the function value at its left edge. In the example, we have defined the function x₁(j) to give us the x-value at the left edge of subinterval j. Then the height of the rectangle is f(x₁(j)).
We have factored the rectangle width out of the sum, so our sum is simply the heights of the left edges of the 6 subintervals. Multiplying that sum by the subinterval width gives our left sum r₁. (It is not a very good approximation of the integral.)
The second and third attachments show a <em>right sum</em> (r₂) and a <em>midpoint sum</em> (r₃). The latter is the best of these approximations.
_____
<u>Other Rules</u>
Described above and shown in the graphics are the use of <em>rectangles</em> for elements of the summation. Another choice is the use of <em>trapezoids</em>. For this, the corners of the trapezoid match the function value on both the left and right edges of the subinterval.
Suppose the n subinterval boundaries are at x0, x1, x2, ..., xn, so that the function values at those boundaries are f(x0), f(x1), f(x2), ..., f(xn). Using trapezoids, the area of the first trapezoid would be ...
a1 = (f(x0) +f(x1))/2·∆x . . . . where ∆x is the subinterval width
a2 = (f(x1) +f(x2))/2·∆x
We can see that in computing these two terms, we have evaluated f(x1) twice. We also see that f(x1)/2 contributes twice to the overall sum.
If we collapse the sum a1+a2+...+an, we find it is ...
∆x·(f(x0)/2 + f(x1) +f(x2) + ... +f(x_n-1) + f(xn)/2)
That is, each function value except the first and last contributes fully to the sum. When we compute the sum this way, we say we are using the <em>trapezoidal rule</em>.
If the function values are used to create an <em>approximating parabola</em>, a different formula emerges. That formula is called <em>Simpson's rule</em>. That rule has different weights for alternate function values and for the end values. The formulas are readily available elsewhere, and are beyond the scope of this answer.
_____
<em>Comment on mechanics</em>
As you can tell from the attachments, it is convenient to let a graphing calculator or spreadsheet compute the sum. If you need to see the interval boundaries and the function values, a spreadsheet may be preferred.