Answer:
Media: 167.88 cm
Mediana: 167.6 cm
Modo: 166.67 cm
Step-by-step explanation:
Hola!
La variable de interés es:
X: estatura de un alumno de noveno año de educación básica.
<u>1)</u>
Primero debes ordenar los datos de menor a mayor y contar cuantos de ellos corresponden dentro de cada intervalo determinado, por ejemplo, el primer intervalo es:
[160;164)
Los intervalos están definidos con el límite inferior cerrado, es decir que incluye el valor de dicho límite, y el límite inferior abierto, es decir, que ese valor no está incluido en el intervalo.
160,160,160,161,162,163,164,165,165,165,165,166,167,167,167,167,168,168,168,169,170, 170, 170,171,173,173,173,175,175,176.
f(1)= 6 (seis valores de estatura corresponden a este intervalo)
La sumatoria de todas las frecuencias absolutas debe dar por resultado el total de observaciones n= 30
Para el segundo intervalo [164;168)
f(2)= 10
<u>2)</u>
hi representa la frecuencia relativa simple y esta se calcula como fi/n
Por ejemplo para el primer intervalo:
h(1)= f(1)/n= 6/30= 0.20
Esta indica la proporción de que las alturas estén entre 160 y 164 cm.
En porcentaje se expresa como hi*100, para el primer intervalo: 0.20*100)= 20%
Para el segundo intervalo h(2)= f(2)/n= 10/30= 0.33 y su porcentaje es 33%
Como indican la proporción de cada categoría de la distribución, la sumatoria de las frecuencias relativas simples de todas las categorías debe ser 1.
<u>3)</u>
Como lo dice su nombre, esta frecuencia es acumulada y se calcula como la sumatoria de las frecuencias absolutas simples, para el primer intervalo, dado que previo a él no hay "nada" es igual a la frecuencia absoluta simple:
F(1)= f(1)
Para el segundo intervalo, es la frecuencia absoluta simple del primer intervalo más la frecuencia relativa simple del segundo intervalo:
F(2)= f(1) + f(2)= 6 + 10= 16
<u>4)</u>
Esta frecuencia también representa la sumatoria de las frecuencias relativas simples.
H(1)= h(1)= 0.20 como previo al primer intervalo no existe distribución definida, la frecuencia relativa acumulada es igual a la frecuencia relativa simple.
Para el segundo intervalo la frecuencia relativa acumulada es:
H(2)= h(1)+h(2)?= 0.20+0.33= 0.57
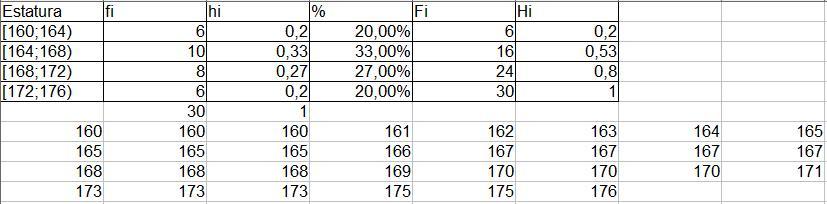
Adjunta a la respuesta encontrarás la tabla completa.
5)
Como no específica medidas de tendencia central requeridas, voy a calcular la media, mediana y modo utilizando la tabla.
<u>Media</u>
X[barra]= (∑x'fi)/n= ∑x'*hi
Dónde x' representa la marca de clase de cada intervalo. Para calcular la marca de clase de los intervalos debes realizar un promedio entre sus límites y su valor siempre debe encontrarse dentro de los límites del intervalo. Si no es así, has cometido un error de cálculos:
(Limite inferior + Limite superior)/2
1. [160;164) x₁'= (160+164)/2= 162
2. [164;168) x₂'= 166
3. [168;172) x₃'= 170
4. [172;176) x₄'= 174
Una vez que calculaste las marcas de clase, puedes calcular la media:
X[barra]= ∑x'*hi= (162*0.20)+(166*0.33)+(170*0.27)+(174*0.20)= 167.88 cm
<u>Mediana:</u>
La mediana es el valor de la variable que divide a la muestra en dos (50%-50%).
Para poder calcularla primero debes identificar su posición, en este tipo de presentación, debes identificar el intervalo en el que se encuentra incluida la mediana.
Para muestras pares, la posición de la mediana se calcula como:
PosMe= n/2= 30/2= 15
Esto significa que la mediana corresponde a la 15va observación de la muestra, observando la columna de las frecuencias absolutas (simples o acumuladas) debes identificar cual es el intervalo de la mediana:
Al segundo intervalo se corresponde una frecuencia acumulada de 16, lo que significa que la posición de la mediana está incluida en este intervalo:
[164;168)
Entonces puedes calcular la mediana como:
Dónde
Li: es el límite inferior del intervalo de mediana.
c: es la amplitud del intervalo
F₍i₋₁₎: frecuencia absoluta acumulada del intervalo anterior al intervalo mediana
fi: frecuencia absoluta del intervalo mediana
Me= 167.6 cm, como puedes notar, el valor de la mediana se encuentra entre los límites del intervalo.
<u>Modo o Moda:</u>
El modo o la moda de una distribución corresponde al valor más observado, es decir, al valor con mayor frecuencia absoluta simple. Al igual que la media, para calcular el modo primero debes identificar el intervalo que lo contiene. En este caso, el intervalo modal será aquel con la mayor frecuencia absoluta simple.
[164;168)
La fórmula para calcular el modo es:
Li: es el límite inferior del intervalo modal
c: es la amplitud del intervalo
: es la frecuencia absoluta simple del intervalo modal.
: es la frecuencia absoluta simple del intervalo anterior al intervalo modal.
: es la frecuencia absoluta simple del intervalo posterior al intervalo modal.
Md= 166.67 cm
¡Espero que tengas un buen día!