Is this ordered pair a solution to the system of linear equations? Yes or no and why or why not?

Use the long division method to find the result when x^3+9x² +21x +9 is divided<br> by x+3

Serhud [2]

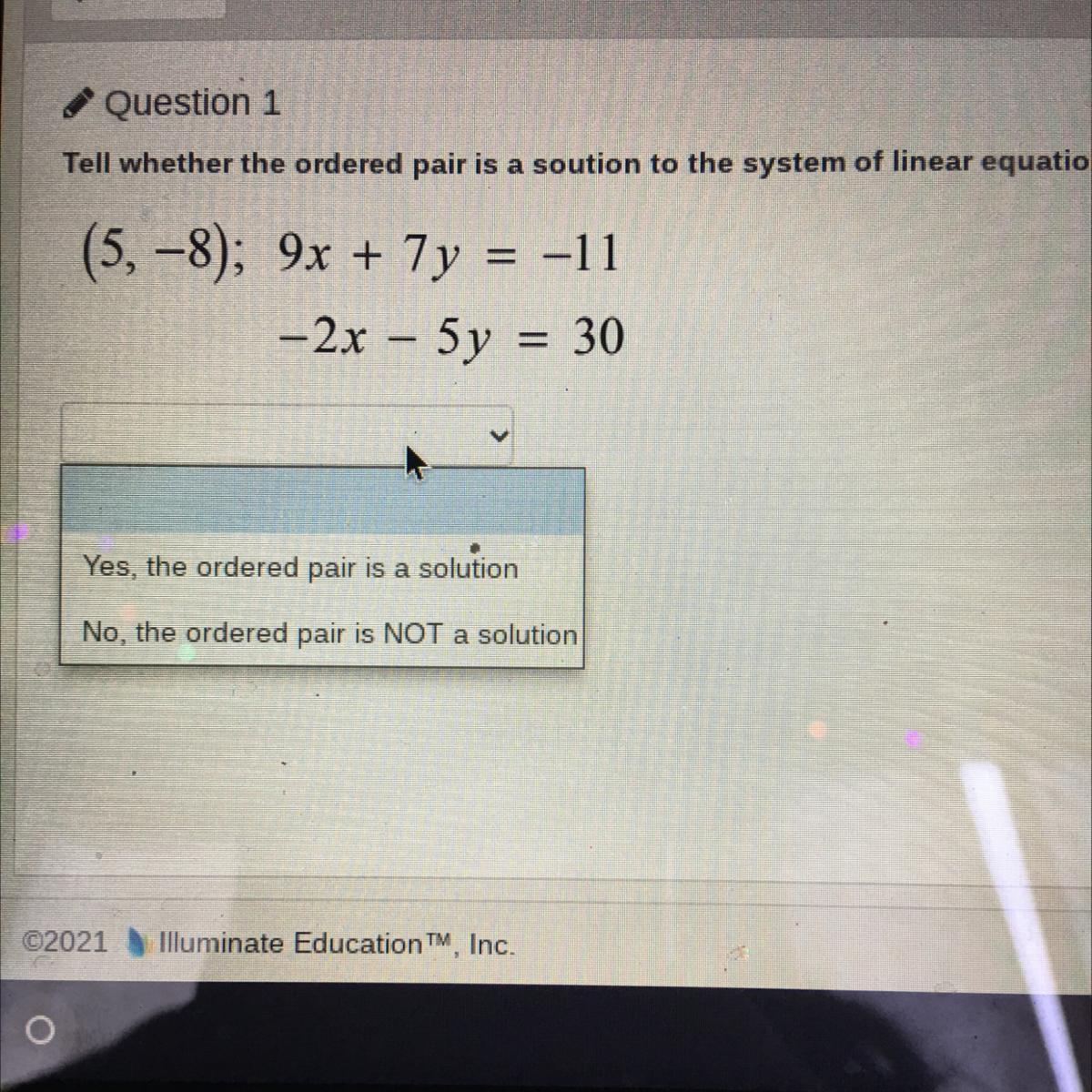
Answer:

x^3 + 9 x^2 + 21 x + 9 = (x^2 + 6 x + 3)×(x + 3) + 0

Step-by-step explanation:

Set up the polynomial long division problem with a division bracket, putting the numerator inside and the denominator on the left:

x + 3 | x^3 | + | 9 x^2 | + | 21 x | + | 9

To eliminate the leading term of the numerator, x^3, multiply x + 3 by x^2 to get x^3 + 3 x^2. Write x^2 on top of the division bracket and subtract x^3 + 3 x^2 from x^3 + 9 x^2 + 21 x + 9 to get 6 x^2 + 21 x + 9:

| | | x^2 | | | |

x + 3 | x^3 | + | 9 x^2 | + | 21 x | + | 9

| -(x^3 | + | 3 x^2) | | | |

| | | 6 x^2 | + | 21 x | + | 9

To eliminate the leading term of the remainder of the previous step, 6 x^2, multiply x + 3 by 6 x to get 6 x^2 + 18 x. Write 6 x on top of the division bracket and subtract 6 x^2 + 18 x from 6 x^2 + 21 x + 9 to get 3 x + 9:

| | | x^2 | + | 6 x | |

x + 3 | x^3 | + | 9 x^2 | + | 21 x | + | 9

| -(x^3 | + | 3 x^2) | | | |

| | | 6 x^2 | + | 21 x | + | 9

| | | -(6 x^2 | + | 18 x) | |

| | | | | 3 x | + | 9

To eliminate the leading term of the remainder of the previous step, 3 x, multiply x + 3 by 3 to get 3 x + 9. Write 3 on top of the division bracket and subtract 3 x + 9 from 3 x + 9 to get 0:

| | | x^2 | + | 6 x | + | 3

x + 3 | x^3 | + | 9 x^2 | + | 21 x | + | 9

| -(x^3 | + | 3 x^2) | | | |

| | | 6 x^2 | + | 21 x | + | 9

| | | -(6 x^2 | + | 18 x) | |

| | | | | 3 x | + | 9

| | | | | -(3 x | + | 9)

| | | | | | | 0

The quotient of (x^3 + 9 x^2 + 21 x + 9)/(x + 3) is the sum of the terms on top of the division bracket. Since the final subtraction step resulted in zero, x + 3 exactly divides x^3 + 9 x^2 + 21 x + 9 and there is no remainder.

| | | x^2 | + | 6 x | + | 3 | (quotient)

x + 3 | x^3 | + | 9 x^2 | + | 21 x | + | 9 |

| -(x^3 | + | 3 x^2) | | | | |

| | | 6 x^2 | + | 21 x | + | 9 |

| | | -(6 x^2 | + | 18 x) | | |

| | | | | 3 x | + | 9 |

| | | | | -(3 x | + | 9) |

| | | | | | | 0 | (remainder) invisible comma

(x^3 + 9 x^2 + 21 x + 9)/(x + 3) = (x^2 + 6 x + 3) + 0

Write the result in quotient and remainder form:

Answer: Set up the polynomial long division problem with a division bracket, putting the numerator inside and the denominator on the left:

x + 3 | x^3 | + | 9 x^2 | + | 21 x | + | 9

To eliminate the leading term of the numerator, x^3, multiply x + 3 by x^2 to get x^3 + 3 x^2. Write x^2 on top of the division bracket and subtract x^3 + 3 x^2 from x^3 + 9 x^2 + 21 x + 9 to get 6 x^2 + 21 x + 9:

| | | x^2 | | | |

x + 3 | x^3 | + | 9 x^2 | + | 21 x | + | 9

| -(x^3 | + | 3 x^2) | | | |

| | | 6 x^2 | + | 21 x | + | 9

To eliminate the leading term of the remainder of the previous step, 6 x^2, multiply x + 3 by 6 x to get 6 x^2 + 18 x. Write 6 x on top of the division bracket and subtract 6 x^2 + 18 x from 6 x^2 + 21 x + 9 to get 3 x + 9:

| | | x^2 | + | 6 x | |

x + 3 | x^3 | + | 9 x^2 | + | 21 x | + | 9

| -(x^3 | + | 3 x^2) | | | |

| | | 6 x^2 | + | 21 x | + | 9

| | | -(6 x^2 | + | 18 x) | |

| | | | | 3 x | + | 9

To eliminate the leading term of the remainder of the previous step, 3 x, multiply x + 3 by 3 to get 3 x + 9. Write 3 on top of the division bracket and subtract 3 x + 9 from 3 x + 9 to get 0:

| | | x^2 | + | 6 x | + | 3

x + 3 | x^3 | + | 9 x^2 | + | 21 x | + | 9

| -(x^3 | + | 3 x^2) | | | |

| | | 6 x^2 | + | 21 x | + | 9

| | | -(6 x^2 | + | 18 x) | |

| | | | | 3 x | + | 9

| | | | | -(3 x | + | 9)

| | | | | | | 0

The quotient of (x^3 + 9 x^2 + 21 x + 9)/(x + 3) is the sum of the terms on top of the division bracket. Since the final subtraction step resulted in zero, x + 3 exactly divides x^3 + 9 x^2 + 21 x + 9 and there is no remainder.

| | | x^2 | + | 6 x | + | 3 | (quotient)

x + 3 | x^3 | + | 9 x^2 | + | 21 x | + | 9 |

| -(x^3 | + | 3 x^2) | | | | |

| | | 6 x^2 | + | 21 x | + | 9 |

| | | -(6 x^2 | + | 18 x) | | |

| | | | | 3 x | + | 9 |

| | | | | -(3 x | + | 9) |

| | | | | | | 0 | (remainder) invisible comma

(x^3 + 9 x^2 + 21 x + 9)/(x + 3) = (x^2 + 6 x + 3) + 0

Write the result in quotient and remainder form:

Answer: x^3 + 9 x^2 + 21 x + 9 = (x^2 + 6 x + 3)×(x + 3) + 0

5 0

2 years ago

Which point is located at (4, 1)? On a coordinate plane, point A is 4 units to the right and 1 unit up. Point B is 4 units to th

mr Goodwill [35]

Answer:

Point A is 4 units to the right and 1 unit up. (A).

Step-by-step explanation:

The reason is (4, 1) is (x, y).

x is in a horizontal line while y is in a vertical line.

In x, right is positive while left is negative.

In y, up is positive while down is negative.

7 0

3 years ago

Read 2 more answers

Adam tabulated the values for the average speeds on each day of his road trip as 60.5, 63.2, 54.7, 51.6, 72.3, 70.7, 67.2, and 6

dezoksy [38]

Answer:

The answer is "2.998".

Step-by-step explanation:

In the given question, the answer is "2.998" because the critical region value will be used to divide the value into two-part that is 0.01, in which each of the value that will have to see the values of the degree of freedom that is 7, in column 0.01, that is equal to 2.998.

3 0

3 years ago

Calcium is an essential nutrient for strong bones and for controlling blood pressure and heart beat. Because most of the body’s

irakobra [83]

Answer:

No, because the 95% confidence interval contains the hypothesized value of zero.

Step-by-step explanation:

Hello!

You have the information regarding two calcium supplements.

X₁: Calcium content of supplement 1

n₁= 12

X[bar]₁= 1000mg

S₁= 23 mg

X₂: Calcium content of supplement 2

n₂= 15

X[bar]₂= 1016mg

S₂= 24mg

It is known that X₁~N(μ₁; σ²₁), X₂~N(μ₂;δ²₂) and σ²₁=δ²₂=?

The claim is that both supplements have the same average calcium content:

H₀: μ₁ - μ₂ = 0

H₁: μ₁ - μ₂ ≠ 0

α: 0.05

The confidence level and significance level are to be complementary, so if 1 - α: 0.95 then α:0.05

since these are two independent samples from normal populations and the population variances are equal, you have to use a pooled variance t-test to construct the interval:

[(X[bar]₁-X[bar]₂) ± $t_{n_1+n_2-2;1-\alpha /2}$ * $Sa*\sqrt{\frac{1}{n_1} +\frac{1}{n_2} }$ ]

$t_{n_1+n_2-2;1-/2}= t_{25;0.975}= 2.060$

$Sa= \sqrt{\frac{(n_1-1)S^2_1+(n_2-1)S^2_2}{n_1+n_2-2} }= \sqrt{\frac{11*529+14*576}{12+15-2} } = 23.57$

[(1000-1016)±2.060*23.57* $\sqrt{\frac{1}{12} +\frac{1}{15} }$ ]

[-34.80;2.80] mg

The 95% CI contains the value under the null hypothesis: "zero", so the decision is to not reject the null hypothesis. Then using a 5% significance level you can conclude that there is no difference between the average calcium content of supplements 1 and 2.

I hope it helps!

3 0

3 years ago

Wanda started walking along a path 27 seconds before Dave. Wanda walked at a constant rate of 3 feet per second. Face walked alo

Paladinen [302]

Answer:

54

Step-by-step explanation:

4.5x=3(x+27)

4.5x=3x+81

1.5x=81

x=54

5 0

3 years ago