Answer:
See attachment
Step-by-step explanation:
The sum of a sequence of interest-earning deposits is the sum of a geometric sequence. The formula for that can be used to help work this problem.
First of all, you need to decide if the monthly deposits are at the beginning or end of the month. If they are at the beginning of the month, and the nest egg size is measured at the beginning of the month after the final deposit, then that final deposit earns 1 month's interest. This makes a difference in the value it is necessary to deposit (by that monthly interest factor).
Since the annual interest rate is 3%, the monthly interest rate is 3%/12 = 0.25%. Then each month the previous balance is multiplied by 1+0.25% = 1.0025 and the new deposit added.
If P is the amount of the final (<em>beginning of the month</em>) deposit, the contribution of that last payment to the Nest Egg size is P·1.0025. The payment before that contributes P·1.0025^2. Then the nest egg is the sum of the geometric series whose first term is P·1.0025 and whose common ratio is 1.0025.
In the 35 years between age 25 and age 60, there will be 12·35 = 420 deposits.
The sum of n terms of a geometric series with first term a1 and common ratio r is ...
Sn = a1·(r^n -1)/(r -1)
We want to find the value of P, where a1 = P·r. Then ...
Sn = P·r(r^n -1)/(r -1)
P = Sn/(r(r^n -1)/(r -1))
This could be simplified, but for our purpose we don't need to do that.
You can see that the needed deposit is proportional to the Nest Egg Size (Sn), so we really only need to compute the denominator value once. For the given numbers (values are shown above), this becomes ...
P = Sn/(1.0025(1.0025^420 -1)/0.0025) ≈ Sn/743.4175661
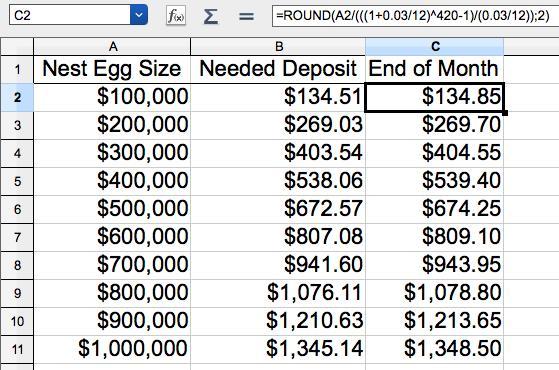
Then the deposit for a $100,000 nest egg is $100,000/743.4175661 ≈ $134.51.
The table in the attachment shows the values for the Nest Egg sizes listed in the problem statement.
___
If the deposit is made at the <em>end of the month</em>, and the Nest Egg Size is measured at the beginning of the next month, the last payment earns no interest, so is simply P, not P·1.0025. Then all the table values are larger by a factor of 1.0025. These values are listed in the column headed "End of Month".
As you might guess, it is convenient to let a spreadsheet do the tedious calculation. The attachment shows the formula used in the highlighted cell along with all the results.
_____
Many graphing calculators or stand-alone apps for phone or tablet are able to do financial calculations. Here, you want the <em>future value (FV)</em> of a sequence of payments (PMT). As you can see in the second attachment, this (TI-84) calculator offers the option of selecting a beginning-of-the-month payment, or an end-of-the-month payment. (We have selected "Begin". The default is generally "End".) By using the largest nest-egg size, we get the greatest number of significant digits in the answer. All other nest egg sizes require proportional payments.
_____
<em>Comment on the use of a spreadsheet</em>
Many spreadsheet programs have a number of financial functions built in. No doubt, there is one that will compute the payment required for a given future value. I didn't look for that. Rather, I just used the formula I knew applied to the problem.