Part 1. For the possible outcomes for the three tosses, we just consider the combinations of heads and tails that can happen. Since HHH and TTT are already supplied, we can just consider:
HTH, THH, HHT
TTH, THT, HTT
We consider the same for four tosses (answer provided in order with respect to the supplied given in the number of outcomes):
HHHH
THHH, HTHH, HHTH, HHHT
HHTT, HTHT, THHT, TTHH, THTH, HTTH
HTTT, THTT, TTHT, TTTH
TTTT
For the total possible outcomes we just add the number of outcomes in the third column. For three tosses we'll have a total of 8 possible outcomes and for four tosses we'll have 16 possible outcomes.
Part 2. From the answers in part 1 we can determine a pattern for the total possible outcomes based on the number of tosses. It's where x is the number of tosses. So for 6 tosses we'll have 64 possible outcomes.
where x is the number of tosses. So for 6 tosses we'll have 64 possible outcomes.
To find how many outcomes would have exactly 4 heads, we determine the number of outcomes with HHHHTT. This will be a simple permutation problem with the equation: . Therefore, there will be 15 outcomes with exactly 4 heads.
. Therefore, there will be 15 outcomes with exactly 4 heads.
We just divide the number of outcomes with exactly 4 heads over all possible outcomes to determine the probability.

ANSWER: The probability would be 0.2.
Part 3-a. A Pascal's triangle is a triangle of numbers where the first and last numbers in every row are 1 and the rows at the middle are determined by getting the sum of the two nearest rows above it. Attached here is an image of the triangle.
We can observe that the pattern of outcomes is exactly like the numbers appearing in the rows of the Pascal's triangle (with the exception of the first row of the triangle)!
Part 3-b. As mentioned earlier, the pattern for the total possible number of outcomes is just where x is the number of tosses. We know this because we are familiar with the fact that the answers supplied in the table in Part 1 are powers of 2.
where x is the number of tosses. We know this because we are familiar with the fact that the answers supplied in the table in Part 1 are powers of 2.
Part 4. We first use the calculator to determine these powers:







We just used the calculator to find these values easily but we can actually use a pattern to find the values. The pattern is evident for the first 5 exponents (0-4). We can see that the first 5 answers all look like the Pascal's triangle values!
Part 5. Yes, you can find the values for the powers of 11 using Pascal's triangle. As stated earlier, the first 5 powers (including 1) are evidently following the pattern. For exponent 5 and up, this is still actually following the triangle but the double digit answers are just carried over to the next digit.
For example, 1 5 10 10 5 1 became 161,051 since the two 10s in the middle had to be carried over.
This pattern will hold true for any powers of 11.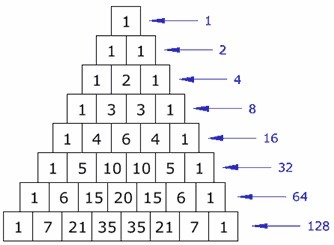
HTH, THH, HHT
TTH, THT, HTT
We consider the same for four tosses (answer provided in order with respect to the supplied given in the number of outcomes):
HHHH
THHH, HTHH, HHTH, HHHT
HHTT, HTHT, THHT, TTHH, THTH, HTTH
HTTT, THTT, TTHT, TTTH
TTTT
For the total possible outcomes we just add the number of outcomes in the third column. For three tosses we'll have a total of 8 possible outcomes and for four tosses we'll have 16 possible outcomes.
Part 2. From the answers in part 1 we can determine a pattern for the total possible outcomes based on the number of tosses. It's
To find how many outcomes would have exactly 4 heads, we determine the number of outcomes with HHHHTT. This will be a simple permutation problem with the equation:
We just divide the number of outcomes with exactly 4 heads over all possible outcomes to determine the probability.
ANSWER: The probability would be 0.2.
Part 3-a. A Pascal's triangle is a triangle of numbers where the first and last numbers in every row are 1 and the rows at the middle are determined by getting the sum of the two nearest rows above it. Attached here is an image of the triangle.
We can observe that the pattern of outcomes is exactly like the numbers appearing in the rows of the Pascal's triangle (with the exception of the first row of the triangle)!
Part 3-b. As mentioned earlier, the pattern for the total possible number of outcomes is just
Part 4. We first use the calculator to determine these powers:
We just used the calculator to find these values easily but we can actually use a pattern to find the values. The pattern is evident for the first 5 exponents (0-4). We can see that the first 5 answers all look like the Pascal's triangle values!
Part 5. Yes, you can find the values for the powers of 11 using Pascal's triangle. As stated earlier, the first 5 powers (including 1) are evidently following the pattern. For exponent 5 and up, this is still actually following the triangle but the double digit answers are just carried over to the next digit.
For example, 1 5 10 10 5 1 became 161,051 since the two 10s in the middle had to be carried over.
This pattern will hold true for any powers of 11.

5
0