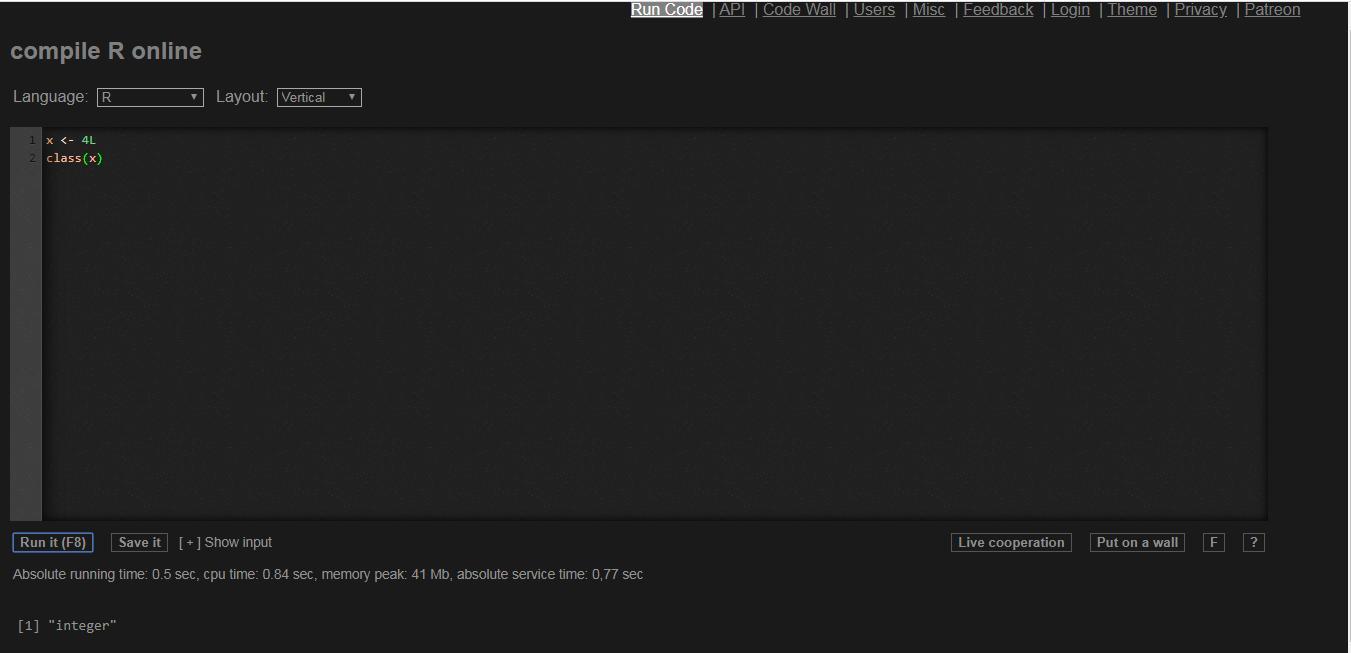
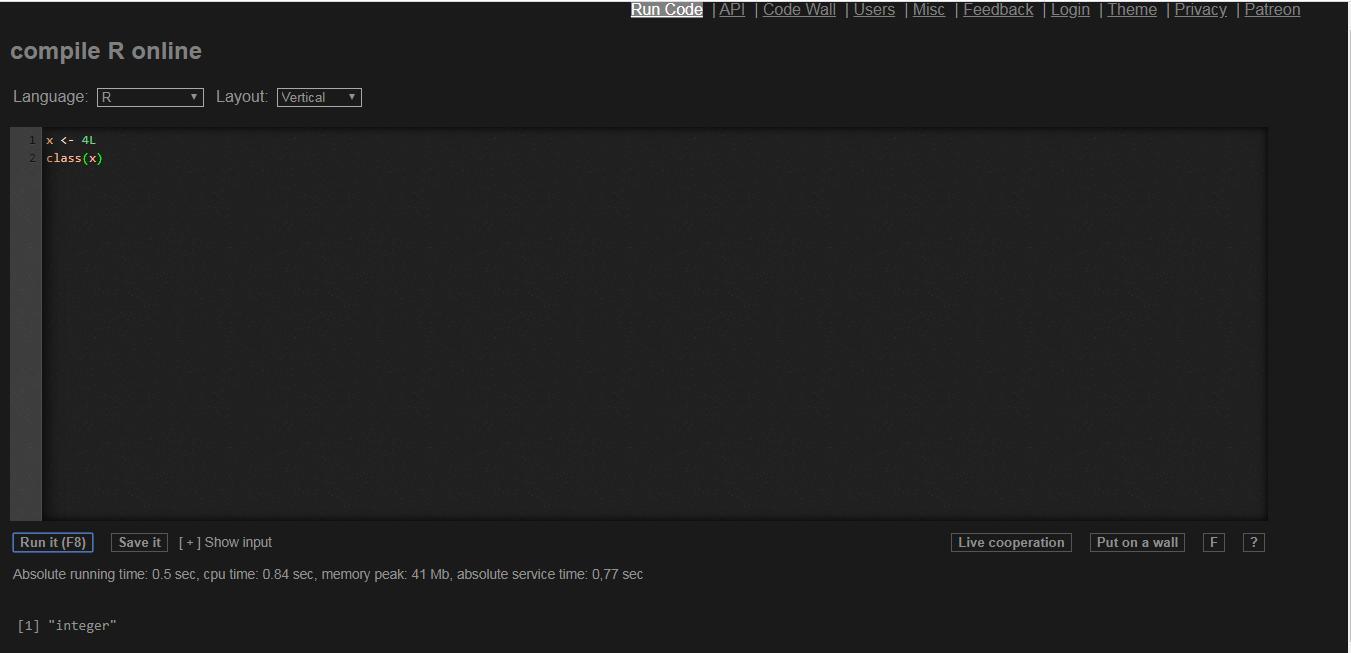
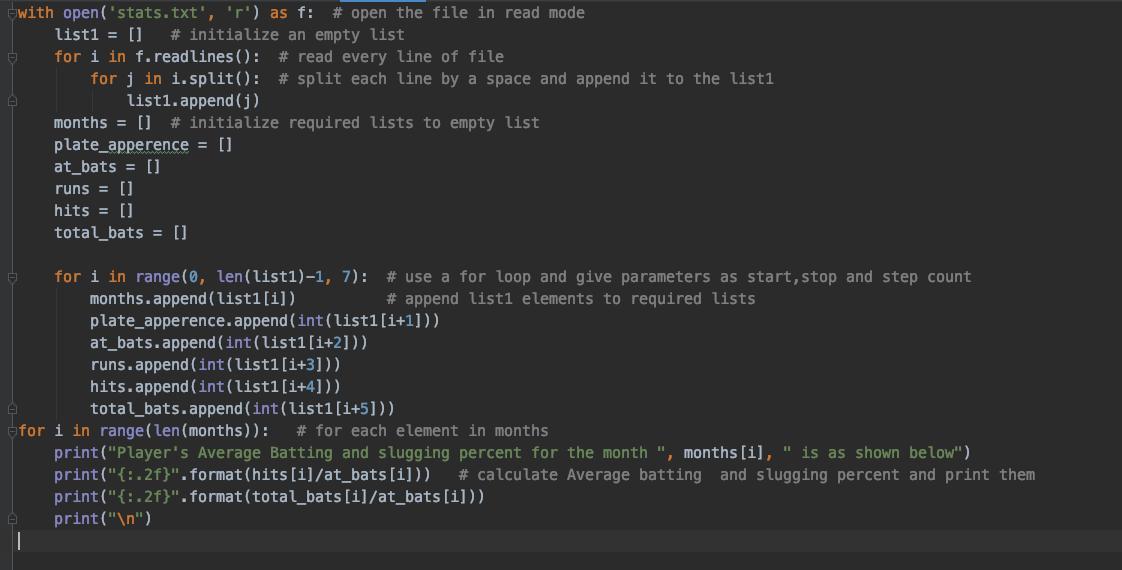
Explanation:
A computer might be described with deceptive simplicity as “an apparatus that performs routine calculations automatically.” Such a definition would owe its deceptiveness to a naive and narrow view of calculation as a strictly mathematical process. In fact, calculation underlies many activities that are not normally thought of as mathematical. Walking across a room, for instance, requires many complex, albeit subconscious, calculations. Computers, too, have proved capable of solving a vast array of problems, from balancing a checkbook to even—in the form of guidance systems for robots—walking across a room.
Before the true power of computing could be realized, therefore, the naive view of calculation had to be overcome. The inventors who laboured to bring the computer into the world had to learn that the thing they were inventing was not just a number cruncher, not merely a calculator. For example, they had to learn that it was not necessary to invent a new computer for every new calculation and that a computer could be designed to solve numerous problems, even problems not yet imagined when the computer was built. They also had to learn how to tell such a general problem-solving computer what problem to solve. In other words, they had to invent programming.
They had to solve all the heady problems of developing such a device, of implementing the design, of actually building the thing. The history of the solving of these problems is the history of the computer. That history is covered in this section, and links are provided to entries on many of the individuals and companies mentioned. In addition, see the articles computer science and supercomputer.
Early history
Computer precursors
The abacus
The earliest known calculating device is probably the abacus. It dates back at least to 1100 BCE and is still in use today, particularly in Asia. Now, as then, it typically consists of a rectangular frame with thin parallel rods strung with beads. Long before any systematic positional notation was adopted for the writing of numbers, the abacus assigned different units, or weights, to each rod. This scheme allowed a wide range of numbers to be represented by just a few beads and, together with the invention of zero in India, may have inspired the invention of the Hindu-Arabic number system. In any case, abacus beads can be readily manipulated to perform the common arithmetical operations—addition, subtraction, multiplication, and division—that are useful for commercial transactions and in bookkeeping.
The abacus is a digital device; that is, it represents values discretely. A bead is either in one predefined position or another, representing unambiguously, say, one or zero.
Analog calculators: from Napier’s logarithms to the slide rule
Calculating devices took a different turn when John Napier, a Scottish mathematician, published his discovery of logarithms in 1614. As any person can attest, adding two 10-digit numbers is much simpler than multiplying them together, and the transformation of a multiplication problem into an addition problem is exactly what logarithms enable. This simplification is possible because of the following logarithmic property: the logarithm of the product of two numbers is equal to the sum of the logarithms of the numbers. By 1624, tables with 14 significant digits were available for the logarithms of numbers from 1 to 20,000, and scientists quickly adopted the new labour-saving tool for tedious astronomical calculations.
Most significant for the development of computing, the transformation of multiplication into addition greatly simplified the possibility of mechanization. Analog calculating devices based on Napier’s logarithms—representing digital values with analogous physical lengths—soon appeared. In 1620 Edmund Gunter, the English mathematician who coined the terms cosine and cotangent, built a device for performing navigational calculations: the Gunter scale, or, as navigators simply called it, the gunter. About 1632 an English clergyman and mathematician named William Oughtred built the first slide rule, drawing on Napier’s ideas. That first slide rule was circular, but Oughtred also built the first rectangular one in 1633. The analog devices of Gunter and Oughtred had various advantages and disadvantages compared with digital devices such as the abacus. What is important is that the consequences of these design decisions were being tested in the real world.
Digital calculators: from the Calculating Clock to the Arithmometer
In 1623 the German astronomer and mathematician Wilhelm Schickard built the first calculator. He described it in a letter to his friend the astronomer Johannes Kepler, and in 1624 . .