Answer:
Step-by-step explanation:
Hello!
You have the information about light bulbs (i believe is their lifespan in hours) And need to organize the information in a frequency table.
The first table will be with a class width of 20, starting with 800. This means that you have to organize all possible observations of X(lifespan of light bulbs) in a class interval with an amplitude of 20hs and then organize the information noting their absolute frequencies.
Example
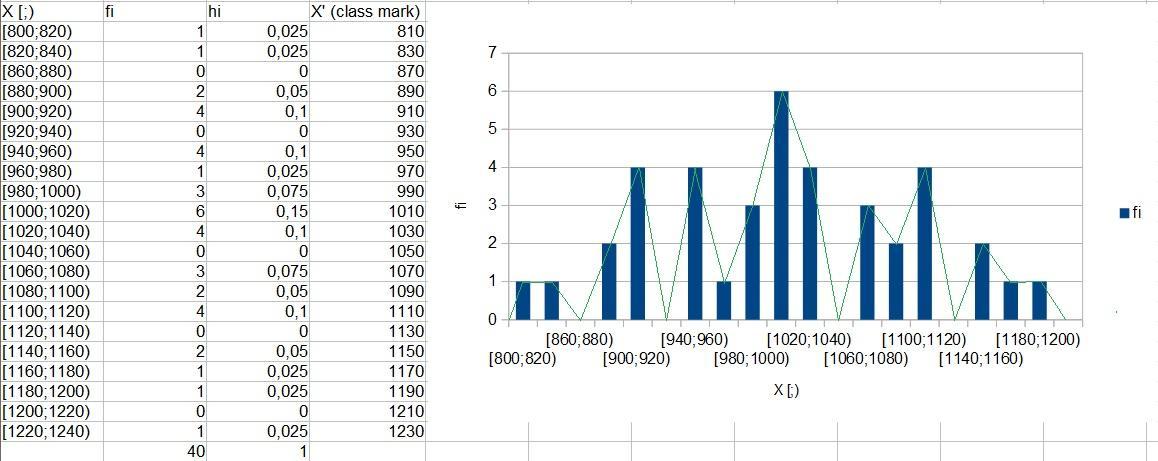
1) [800;820) only one observation classifies for this interval x= 819, so f1: 1
2)[820; 840) only one observation classifies for this interval x= 836, so f2: 1
3)[840;860) no observations are included in this interval, so f3=0
etc... (see attachment)
[ means that the interval is closed and starts with that number
) means that the interval is open, the number is not included in it.
fi: absolute frequency
hi= fi/n: relative frequency
To graph the histogram you have to create the classmark for each interval:
x'= (Upper bond + Lower bond)/2
As you can see in the table, there are several intervals with no observed frequency, this distribution is not uniform least to say symmetric.
To check the symmetry of the distribution is it best to obtain the values of the mode, median and mean.
To see if this frequency distribution has one or more modes you have to identify the max absolute frequency and see how many intervals have it.
In this case, the maximal absolute frequency is fi=6 and only one interval has it [1000;1020)
LB= Lower bond of the modal interval
D₁= fmax - fi of the previous interval
D₂= fmax - fi of the following interval
Ai= amplitude of the modal interval
This distribution is unimodal (Mo= 1012)
The Median for this frequency:
Position of the median= n/2 = 40/2= 20
The median is the 20th fi, using this information, the interval that contains the median is [1000;1020)
LB= Lower bond of the interval of the median
Ai= amplitude of the interval
F(i-1)= acumulated absolute frequency until the previous interval
fi= absolute frequency of the interval
Mean for a frequency distribution:
∑x'*fi= summatory of each class mark by the frequency of it's interval.
∑x'*fi= (810*1)+(230*1)+(870*0)+(890*2)+(910*4)+(930*0)+(950*4)+(970*1)+(990*3)+(1010*6)+(1030*4)+(1050*0)+(1070*3)+(1090*2)+(1110*4)+(1130*0)+(1150*2)+(1170*1)+(1190*1)+(1210*0)+(1230*1)= 40700
Mo= 1012 < Me= 1013.33 < X[bar]= 1017.5
Looking only at the measurements of central tendency you could wrongly conclude that the distribution is symmetrical or slightly skewed to the right since the three values are included in the same interval but not the same number.
*-*-*
Now you have to do the same but changing the class with (interval amplitude) to 100, starting at 800
Example
1) [800;900) There are 4 observations that are included in this interval: 819, 836, 888, 897 , so f1=4
2)[900;1000) There are 12 observations that are included in this interval: 903, 907, 912, 918, 942, 943, 952, 959, 962, 986, 992, 994 , so f2= 12
etc...
As you can see this distribution is more uniform, increasing the amplitude of the intervals not only decreased the number of class intervals but now we observe that there are observed frequencies for all of them.
Mode:
The largest absolute frequency is f(3)=15, so the mode interval is [1000;1100)
Using the same formula as before:
This distribution is unimodal.
Median:
Position of the median n/2= 40/2= 20
As before is the 20th observed frequency, this frequency is included in the interval [1000;1100)
Mean:
∑x'*fi= (850*4)+(950*12)+(1050*15)+(1150*8)+(1250*1)= 41000
X[bar]= 1025 < Me= 1026.67 < Mo= 1030
The three values are included in the same interval, but seeing how the mean is less than the median and the mode, I would say this distribution is symmetrical or slightly skewed to the left.
I hope it helps!