If y = 2x - 8 what is the minimum value of the product xy

Mathematics

2 answers:

Alja [10]3 years ago

6 0

Answer:

the minimum value of product is -8

Step-by-step explanation:

We have been given the function y = 2x-8 and we have to find the minimum value of the xy.

Plugging the value of y in the product

$f(x)=x(2x-8)\\\\f(x)=2x^2-8x$

f(x) represents a upward parabola and we know that for a upward parabola, the minimum point is the vertex.

So in order to find the minimum value we find the y coordinate of the vertex of the parabola.

x-coordinate of the parabola is given by

$-\frac{b}{2a}\\\\=-\frac{-8}{2\cdot2}\\\\=2$

y -coordinate of the parabola is

$y=f(2)=2(2)^2-8(2)\\\\=8-16=-8$

Hence, the vertex is (2,-8)

Therefore, the minimum value of product is -8

pantera1 [17]3 years ago

5 0

Hello :
xy = x(2x-8)
let : f(x) = 2x²-8x
the derivate is : f'(x) = 4x-8
f'(x) = 0 ... x=2
sign f'(x) : -∞ ــــــــــــــــــــــــــ2ـــــــــــــــــــــــ⟶ +∞
-------------- 0 +++++++++
the minimum value of the product xy is the minimum value of f :
f(2) = 2(2)²-8(2) =-8

You might be interested in

Please help ASAP IM IN DESPREATE NEED OF HELP

Advocard [28]

Answer:

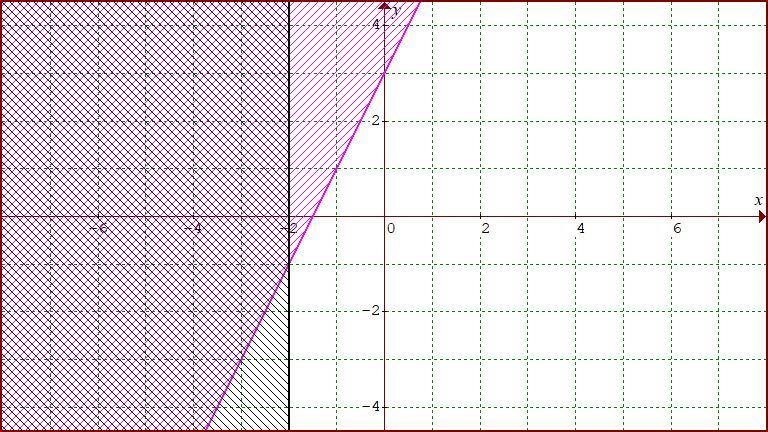
See the attached image for the graph of the first system.

Step-by-step explanation:

Here's how to graph the first system.

Start with the inequality $-y \le -2x-3$ . You can make this easier to work with by multiplying through by -1. Remember to switch the inequality sign when multiplying by a negative number. OK, you get the inequality

$y \ge 2x+3$ .

The graph will be a half-plane -- all the points on one side of a line. The line that is the boundary of the half-plane has an equation: $y=2x+3$ -- just use an = sign instead of the inequality sign.

Graph the line.

The equation of the line is in slope-intercept form: y = mx + b, so you can tell the y-intercept is 3 and the slope is 2 (think of it as a fraction 2/1). Graph the line by going to the point (0, 3) -- the y-intercept -- then use the slope 2/1 interpreted as "rise over run" to go up 2 units and right 1 unit, arriving at the point (1, 5). Draw the line through those points, (0, 3) and (1, 5).

Now you have to decide which side of the line the inequality $y \ge 2x+3$ is describing. To do this, pick a point which is not on the line, plug its coordinates into the inequality; if the result is true, shade the side of the line the point you picked is on (if false, shade the other side!)

An easy point to pick in this case is the origin, (0, 0). Put zeros in for x and y in the inequality, and you'll get the statement $0 \ge 2(0)+3 \, \Rightarrow \, 0 \ge 3$ . That's false, so shade the side of the line not containing the origin. In the image below, the shading is in purple.

All right, now for the other inequality, $x+2\le 0$ . Subtract 2 from both sides and the inequality becomes $x \le -2$ . This, too, graphs as a half-plane whose boundary line has equation $x=-2$ . Graph the line. A line with an equation that has x in it but not y is a vertical line with all its x-coordinates equal to the number on the right side of the equation. This line is vertical and goes through points such as (-2, 0).

Pick a point not on the line (the origin works again). Put the coordinates into the inequality to get $0\le -2$ which is false. Shade the side of the vertical line which does not contain the origin. In the image below, the shading is in black.

Finally, YAY! \o/ , the solutions to the system are all the points in the plane that got shaded twice. In the image, they are the cross-hatched points above the purple line and to left of the black line.

Note: If you get a system with three inequalities, you'll be graphing three half-planes and looking for points that got shaded three times!

Note: One of your questions has the inequalities $x \ge 0$ and $y \ge 0$ in it. These two inequalities say that the x and y coordinates are both positive or zero, confining your attention to Quadrant I in the upper-right part of a graph, above the x-axis and to the right of the y-axis.