Kieran subscribes to a text messaging service on his cell phone. His monthly bill for the service is given by the equation b = 0
2 answers:
You might be interested in
The speed for which Brian iron the shirts is given by:
Rewriting we have:
Then, for each minute, we have the amount of ironed shirt is:
Answer:
At this rate, Brian plans 10/162 of his shirt.
Solution :
Let and
represents the proportions of the seeds which germinate among the seeds planted in the soil containing
and
mushroom compost by weight respectively.
To test the null hypothesis against the alternate hypothesis
.
Let denotes the respective sample proportions and the
represents the sample size respectively.
The test statistic can be written as :
which under 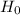follows the standard normal distribution.
We reject 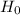at
level of significance, if the P-value
or if
Now, the value of the test statistics = -1.368928
The critical value =
P-value =
= 0.171335
Since the p-value > 0.05 and , so we fail to reject
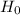at
level of significance.
Hence we conclude that the two population proportion are not significantly different.
Conclusion :
There is not sufficient evidence to conclude that the of the seeds that
with the percent of the
in the soil.
Answer:(-3,-8),(-6,4),(1,-1)
Step-by-step explanation:
Given
Vertices of the triangle are
Coordinates (a,b) when reflected about x-axis is given as (a,-b) i.e. Y coordinate changes its sign