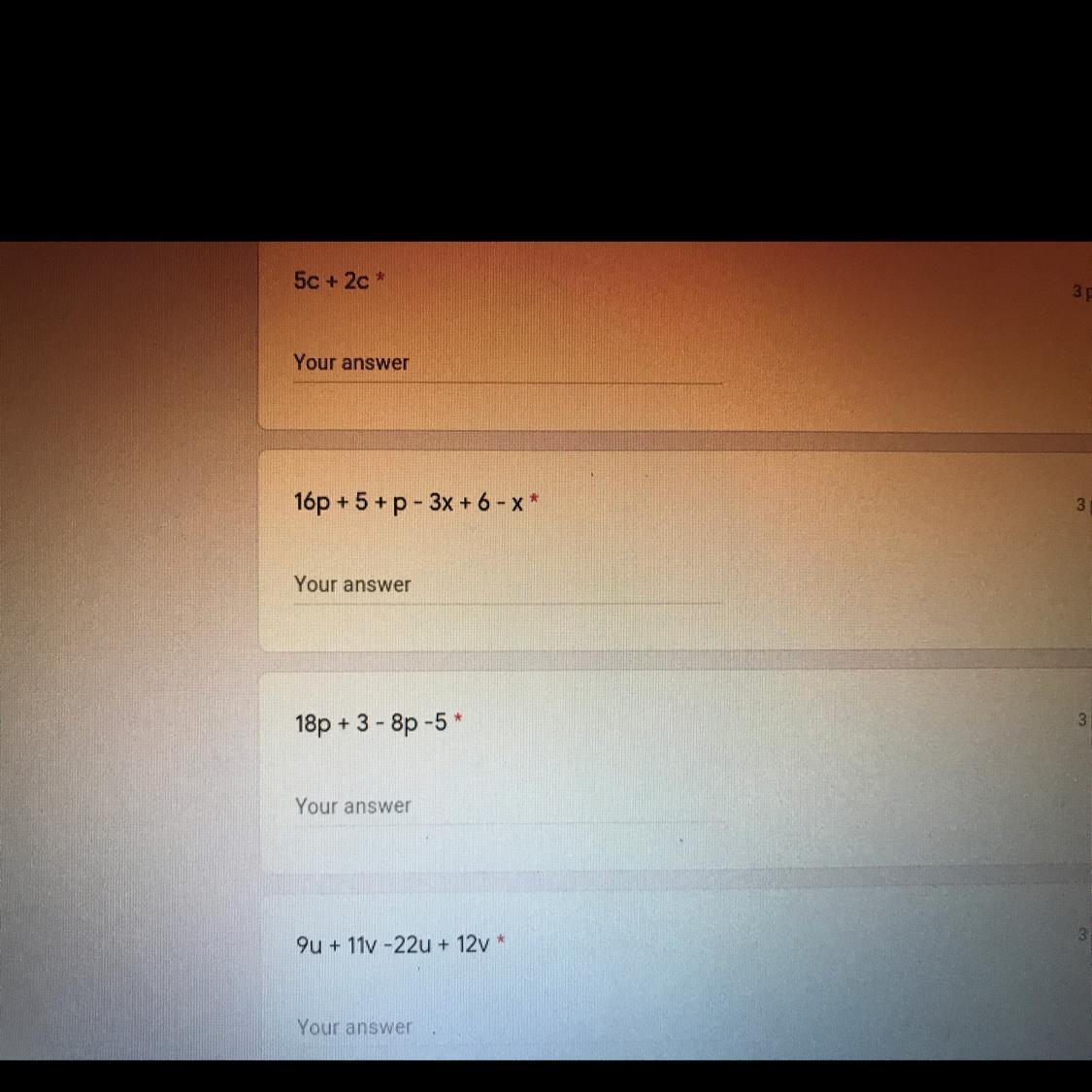
Question Completion:
SubID Memory1 Memory2
1 71 78
2 75 75
3 77 82
4 90 91
5 72 90
6 79 81
7 84 75
8 75 86
9 85 92
10 75 77
11 72 92
12 76 87
13 77 93
14 90 94
15 84 78
16 73 92
17 75 85
18 87 86
19 75 95
20 70 94
21 72 75
22 90 84
23 81 94
24 87 82
25 90 82
26 87 79
27 78 94
28 78 79
29 70 82
30 81 80
31 80 78
32 90 87
33 83 90
34 81 85
35 73 88
36 82 82
37 84 94
38 85 86
39 77 94
40 82 83
Answer:
Since the mean of Memory1 (reciting method) (79.8) is smaller than the mean of Memory2 (imagery method) (85.5), we can conclude that there is a significant difference in memory performance between the reciting method and the imagery method.
Step-by-step explanation:
a) Data and Calculations:
SubID Memory1 Memory2
1 71 78
2 75 75
3 77 82
4 90 91
5 72 90
6 79 81
7 84 75
8 75 86
9 85 92
10 75 77
11 72 92
12 76 87
13 77 93
14 90 94
15 84 78
16 73 92
17 75 85
18 87 86
19 75 95
20 70 94
21 72 75
22 90 84
23 81 94
24 87 82
25 90 82
26 87 79
27 78 94
28 78 79
29 70 82
30 81 80
31 80 78
32 90 87
33 83 90
34 81 85
35 73 88
36 82 82
37 84 94
38 85 86
39 77 94
40 82 83
Total 3,193 3,421
Mean 79.8 85.5
Difference in means = 5.7 (85.5 - 79.8)