The instructions for these problems seem incomplete. I'm assuming your teacher wants you to find the equation of each parabola.
===============================================================
Problem 1
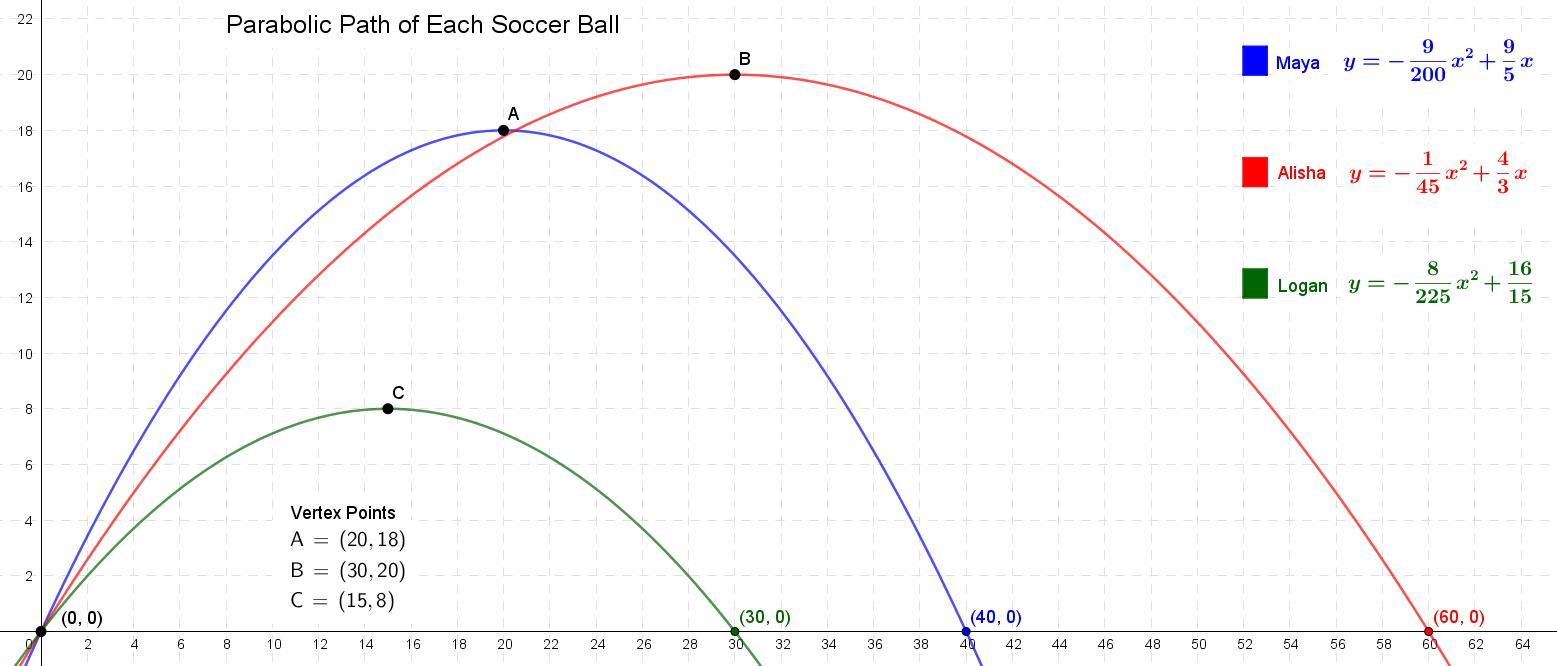
Let's place Maya at the origin (0,0) on the xy coordinate grid. We'll have her kick to the right along the positive x axis direction.
The ball lands 40 feet away from her after it sails through the air. So the ball lands at (40,0). At the halfway point is the vertex (due to symmetry of the parabola), so it occurs when x = 40/2 = 20. The ball is at a height of 18 feet here, which means the vertex location is (20,18).
The vertex being (h,k) = (20,18) leads to...
Let's plug in another point on this parabola, say the origin point. Then we'll solve for the variable 'a'.
So we can then say,
The final equation is in the form where
x = horizontal distance the ball is from Maya
y = vertical distance the ball is from Maya
Maya is placed at the origin (0,0)
The graph is shown below. Refer to the blue curve.
===============================================================
Problem 2
We could follow the same steps as problem 1, but I'll take a different approach.
Like before, the kicker is placed at the origin and will aim to the right.
Since the ball is on the ground at (0,0), this is one of the x intercepts. The other x intercept is at (60,0) because it lands 60 feet away from the kicker.
The two roots x = 0 and x = 60 lead to the factors x and x-60 respectively.
We then end up with the factorized form where the 'a' is in the same role as before. It's the leading coefficient.
To find 'a', we'll plug in the coordinates of the vertex point (30,20). The 30 is due to it being the midpoint of x = 0 and x = 60. The 20 being the height of the ball at this peak.
Let's use this to find the standard form of the parabola.
Refer to the red curve in the graph below.
===============================================================
Problem 3
We can use either method (similar to problem 1 or problem 2). The second problem's method is probably faster.
Logan is placed at (0,0) and kicks to the right. The ball lands at (30,0). Those x intercepts are x = 0 and x = 30 respectively, which lead to the factors x and x-30. This leads to
The midpoint of (0,0) and (30,0) is (15,0). Eight feet above this midpoint is the location (15,8) which is the vertex. Plug in (x,y) = (15,8) and solve for 'a'
So,
The graph is the green curve in the diagram below.
Like with the others, x and y represent the horizontal and vertical distance the ball is from the kicker. The kicker is placed at the origin (0,0).
Once we know the equation of the parabola, we can answer questions like: "how high up is the ball when it is horizontally 10 feet away?". We do this by plugging in x = 10 and computing y.
Side note: We assume that there isn't any wind. Otherwise, the wind would slow the ball down and it wouldn't be a true parabola. However, that greatly complicates the problem.