The answer is D
132,400 divided by 4 is 33,100
If you had the same questions as me here's the rest of the answers to the test
To all who see's this in the future You Are Welcome!
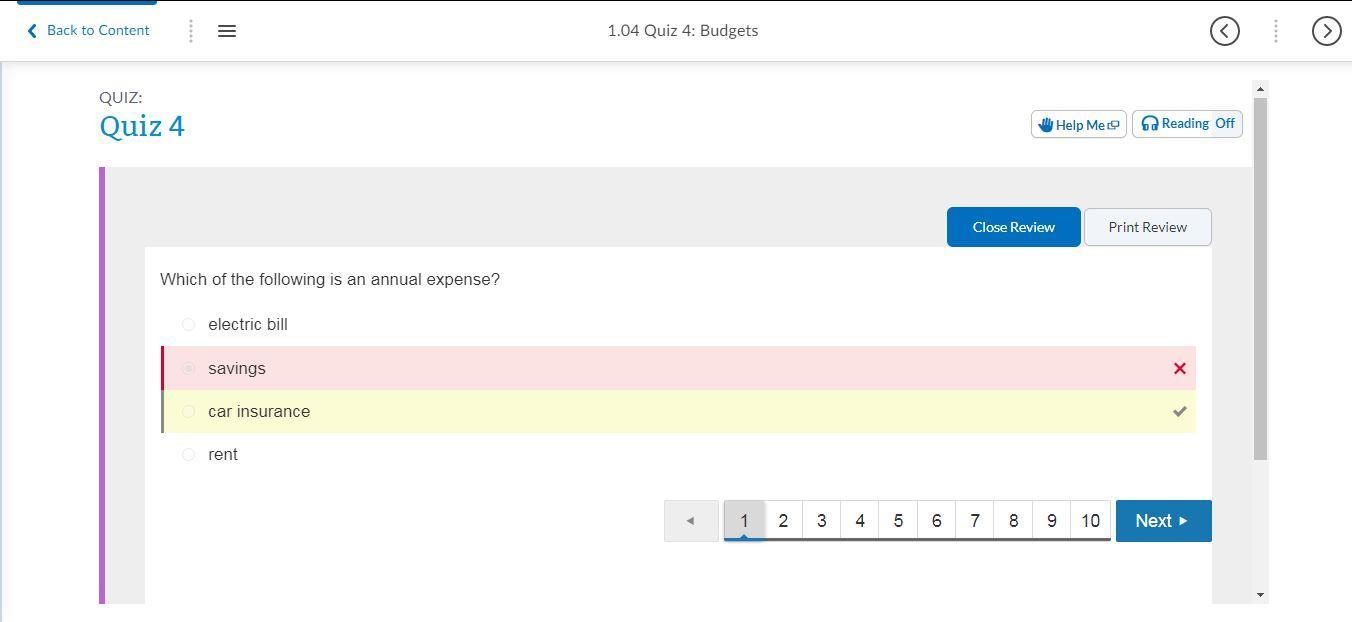
1. Which of the following is an annual expense?
electric bill
savings
car insurance* (Correct Answer)
rent
2. You spent these amounts on gasoline for the past four months: $67, $78, $53, $89.
What should you budget for gasoline this month?
$89
$72* (Correct Answer)
$70
$53
3. Home insurance costs $468 annually.
How much should you budget monthly for home insurance?
$58
$45
$40
$39* (Correct Answer)
4. You spend $890 a month on living expenses.
If your monthly income is $1500, what percent of your income do you spend on living expenses?
Round to the nearest tenth percent.
59.3%* (Correct Answer)
37%
16.9%
5.93%
5. Which of the following is a fixed expense?
transportation
water bill
car payment* (Correct Answer)
clothing
6. Mary's Monthly Budget
Income $617 Fixed Expenses
Rent $150
Living Expenses Emergency Fund $30
Electric $30 Annual Expenses
Transportation $60 Car Insurance $850
Food $200 Books $400
Entertainment $40 Tuition (parents pay)
What are the total living expenses?
$330* (Correct Answer)
$360
$510
$945
7. Mary's Monthly Budget
Income $617 Fixed Expenses
Rent $150
Living Expenses Emergency Fund $30
Electric $30 Annual Expenses
Transportation $60 Car Insurance $850
Food $200 Books $400
Entertainment $40 Tuition (parents pay)
What is the monthly share of the annual expenses?
$100
$104* (Correct Answer)
$114
$150
8. Mary's Monthly Budget
Income $617 Fixed Expenses
Rent $150
Living Expenses Emergency Fund $30
Electric $30 Annual Expenses
Transportation $60 Car Insurance $850
Food $200 Books $400
Entertainment $40 Tuition (parents pay)
What describes the status of Mary's budget?
it is in deficit
it is balanced
it is in surplus* (Correct Answer)
9. Mary's Monthly Budget
Income $617 Fixed Expenses
Rent $150
Living Expenses Emergency Fund $30
Electric $30 Annual Expenses
Transportation $60 Car Insurance $850
Food $200 Books $400
Entertainment $40 Tuition (parents pay)
The fixed expenses are what percent of Mary's income?
34.3%
29.2%* (Correct Answer)
20.1%
2.9%
10. The pie chart represents the Chong family budget.
If their monthly income is $4670, how much do they spend on living expenses?
$1168
$1205
$1635* (Correct Answer)
$1868
11. Cost of Raising a Child In 8 Years
Birth to 5 y old $91,200
5 to 18 y old $167,000
4 y Public College $35,000
4 y Private College $132,400
If the Ball family has a child in eight years, how much can they expect to spend to raise the child, per year, from birth to five years of age?
$22,800
$21,530
$20,890
$18,240* (Correct Answer)
12. Cost of Raising a Child In 8 Years
Birth to 5 y old $91,200
5 to 18 y old $167,000
4 y Public College $35,000
4 y Private College $132,400
How much can the Ball family expect to pay, per year, to raise the child from birth to 18 years of age?
$12,846
$13,458
$14,344* (Correct Answer)
$15,188
13. Cost of Raising a Child In 8 Years
Birth to 5 y old $91,200
5 to 18 y old $167,000
4 y Public College $35,000
4 y Private College $132,400
How much can the Ball family expect to pay per year for tuition to a private college?
$8750
$9250
$32,200
$33,100* (Correct Answer)
14. Let the equation C = 2.32 N + 34,180 represent the cost of raising a child, C, on an income, N.
If the Corlone family has an income of $40,000 annually, what is the expect cost of raising a child?
$122,460
$123,540
$125,620
$126,980* (Correct Answer)
15. Let C = 2.32 N + 34180 represent the cost, C, of raising a child to 18 y on an income, N.
If the cost is $200,000, what is the income?
$71,474* (Correct Answer)
$72,382
$73,521
$74,856