All categories

1 year ago

Write an expression for the sequence of operations described below.

1 answer:

6 0

Given question ,

Raise v to the 5th power then triple the result

The expression is as follows :

$v ^{5}$

Tripling , $(v^5)^{3}$

You might be interested in

How many times does 16 go into 109

schepotkina [342]

Answer:

Step-by-step explanation:

109/16= 6.8125 times

4 0

3 years ago

Hypothesis Testing

Yuri [45]

Answer:

Problem 1: We conclude that less than or equal to 50% of adult Americans without a high school diploma are worried about having enough saved for retirement.

Problem 2: We conclude that the volume of Google stock has changed.

Step-by-step explanation:

Problem 1:

We are given that in a recent survey conducted by Pew Research, it was found that 156 of 295 adult Americans without a high school diploma were worried about having enough saved for retirement.

Let p = proportion of adult Americans without a high school diploma who are worried about having enough saved for retirement

So, Null Hypothesis, 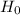$H_0$ : p $\leq$ 50% {means that less than or equal to 50% of adult Americans without a high school diploma are worried about having enough saved for retirement}

Alternate Hypothesis, $H_A$ : p > 50% {means that a majority of adult Americans without a high school diploma are worried about having enough saved for retirement}

This is a right-tailed test.

The test statistics that would be used here is One-sample z-test for proportions;

T.S. = $\frac{\hat p-p}{\sqrt{\frac{p(1-p)}{n} } }$ ~ N(0,1)

where, $\hat p$ = sample proportion of adult Americans who were worried about having enough saved for retirement = $\frac{156}{295}$ = 0.53

n = sample of adult Americans = 295

So, the test statistics = $\frac{0.53-0.50}{\sqrt{\frac{0.50(1-0.50)}{295} } }$

= 1.03

The value of z-test statistics is 1.03.

Also, the P-value of the test statistics is given by;

P-value = P(Z > 1.03) = 1 - P(Z $\leq$ 1.03)

= 1 - 0.8485 = 0.1515

Now, at a 0.05 level of significance, the z table gives a critical value of 1.645 for the right-tailed test.

Since the value of our test statistics is less than the critical value of z as 1.03 < 1.645, so we insufficient evidence to reject our null hypothesis as it will not fall in the rejection region.

Therefore, we conclude that less than or equal to 50% of adult Americans without a high school diploma are worried about having enough saved for retirement.

Problem 2:

We are given that a random sample of 35 trading days in 2014 resulted in a sample mean of 3.28 million shares with a standard deviation of 1.68 million shares.

Let $\mu$ = mean daily volume in Google stock

So, Null Hypothesis, 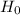$H_0$ : $\mu$ = 5.44 million shares {means that the volume of Google stock has not changed}

Alternate Hypothesis, $H_A$ : $\mu$ $\neq$ 5.44 million shares {means that the volume of Google stock has changed}

This is a two-tailed test.

The test statistics that would be used here is One-sample t-test statistics because we don't know about the population standard deviation;

T.S. = $\frac{\bar X-\mu}{\frac{s}{\sqrt{n} } }$ ~ $t_n_-_1$

where, $\bar X$ = sample mean volume in Google stock = 3.28 million shares

s = sample standard deviation = 1.68 million shares

n = sample of trading days = 35

So, the test statistics = $\frac{3.28-5.44}{\frac{1.68}{\sqrt{35} } }$ ~ $t_3_4$

= -7.606

The value of t-test statistics is -7.606.

Also, the P-value of the test statistics is given by;

P-value = P( $t_3_4$ < -7.606) = Less than 0.05%

Now, at a 0.05 level of significance, the t table gives a critical value of -2.032 and 2.032 at 34 degrees of freedom for the two-tailed test.

Since the value of our test statistics doesn't lie within the range of critical values of t, so we sufficient evidence to reject our null hypothesis as it will fall in the rejection region.

Therefore, we conclude that the volume of Google stock has changed.

8 0

3 years ago

Regular Sire (12 ounces)

worty [1.4K]

0.27 per ounce for regular
And
0.26 per ounce for family

7 0

3 years ago

I WILL MARK BRAINLIEST IF HELP!!

aksik [14]

Answer:

a 20 X 40 X x

b just a guess but 2 centimeters

c 1600 or 800 depending on what x is

3 0

3 years ago

Barry's family drove 843 mi to see his grandparents. On the first day, they drove 483 mi. On the second day, how long did it tak

sergey [27]

843 - 483 = 360
360 ÷ 60 = 6
It took Barry's family 6 hours to drive to their grandparent's house

6 0

3 years ago