Given:
Ship M travels E 15 km, then N35E 27 km. Its sub travels down 48° 2 km from that location.
Ship F travels S75E 20 km, then N25E 38 km. The treasure is expected to be at this location 2.18° below horizontal from the port.
Find:
1a. The distance from port to Ship M
1b. The distance from port to the sub
1c. The angle below horizontal from the port to the sub
2a. The distance from port to Ship F
2b. The depth to the expected treasure location
2c. The distance from port to the expected treasure location
Solution:
It can be helpful to draw diagrams. See the attached. The diagram for depth is not to scale.
There are several ways this problem can be worked. A calculator that handles vectors (as many graphing calculators do) can make short work of it. Here, we will use the Law of Cosines and the definitions of Tangent and Cosine.
Part 1
1a. We are given sides 15 and 27 of a triangle and the included angle of 125°. Then the distance (m) from the port to the ship is given by the Law of Cosines as
m² = 15² +27² -2·15·27·cos(125°) ≈ 1418.60
m ≈ 37.66
The distance from port to Ship M is 37.66 km.
1b. The distance just calculated is one side of a new triangle with other side 2 km and included angle of 132°. Then the distance from port to sub (s) is given by the Law of Cosines as
s² = 1418.60 +2² -2·37.66·2·cos(132°) ≈ 1523.41
s ≈ 39.03
The distance from port to the sub is 39.03 km.
1c. The Law of Sines can be used to find the angle of depression (α) from the port. That angle is opposite the side of length 2 in the triangle of 1b. The 39.03 km side is opposite the angle of 132°. So, we have the relation
sin(α)/2 = sin(132°)/39.03
α = arcsin(2·sin(132°)/39.03) ≈ 2.18°
The angle below horizontal from the port to the sub is 2.18°.
Part 2
2a. We are given sides 20 and 38 of a triangle and the included angle of 100°. Then the distance (f) from the port to the ship is given by the Law of Cosines as
f² = 20² +38² -2·20·38·cos(100°) ≈ 2107.95
f ≈ 45.91
The distance from port to Ship F is 45.91 km.
2b. The expected treasure location is at a depth that is 2.18° below the horizontal from the port. The tangent ratio for an angle is the ratio of the opposite side (depth) to the adjacent side (distance from F to port), so we have
tan(2.18°) = depth/45.91
depth = 45.91·tan(2.18°) ≈ 1.748
The depth to the expected treasure location is 1.748 km.
2c. The distance from port to the expected treasure location is the hypotenuse of a right triangle. The cosine ratio for an angle is the ratio of the adjacent side to the hypotenuse, so we have
cos(2.18°) = (port to F distance)/(port to treasure distance)
(port to treasure distance) = 45.91 km/cos(2.18°) ≈ 45.95
The distance from the port to the expected treasure is 45.95 km.
Part 3
It seems the Mach 5 Mimi is the ship most likely to have found the treasure. That one seems ripe for attack. Its crew goes to a location that is 2.18° below horizontal. The crew of the FTFF don't have any idea where they are going. (Of course, the pirate ship would have no way of knowing if it is only observing surface behavior.)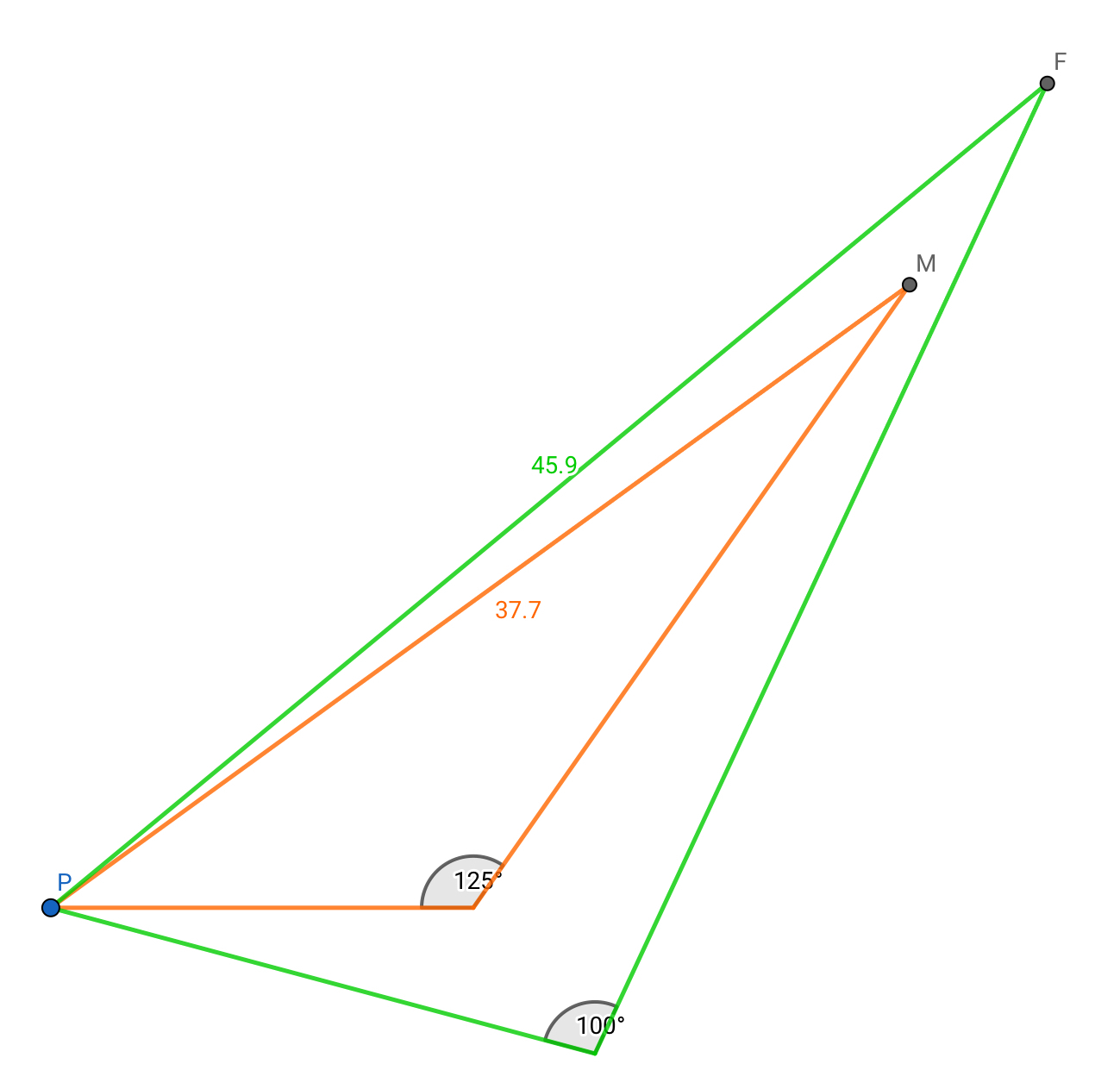
Ship M travels E 15 km, then N35E 27 km. Its sub travels down 48° 2 km from that location.
Ship F travels S75E 20 km, then N25E 38 km. The treasure is expected to be at this location 2.18° below horizontal from the port.
Find:
1a. The distance from port to Ship M
1b. The distance from port to the sub
1c. The angle below horizontal from the port to the sub
2a. The distance from port to Ship F
2b. The depth to the expected treasure location
2c. The distance from port to the expected treasure location
Solution:
It can be helpful to draw diagrams. See the attached. The diagram for depth is not to scale.
There are several ways this problem can be worked. A calculator that handles vectors (as many graphing calculators do) can make short work of it. Here, we will use the Law of Cosines and the definitions of Tangent and Cosine.
Part 1
1a. We are given sides 15 and 27 of a triangle and the included angle of 125°. Then the distance (m) from the port to the ship is given by the Law of Cosines as
m² = 15² +27² -2·15·27·cos(125°) ≈ 1418.60
m ≈ 37.66
The distance from port to Ship M is 37.66 km.
1b. The distance just calculated is one side of a new triangle with other side 2 km and included angle of 132°. Then the distance from port to sub (s) is given by the Law of Cosines as
s² = 1418.60 +2² -2·37.66·2·cos(132°) ≈ 1523.41
s ≈ 39.03
The distance from port to the sub is 39.03 km.
1c. The Law of Sines can be used to find the angle of depression (α) from the port. That angle is opposite the side of length 2 in the triangle of 1b. The 39.03 km side is opposite the angle of 132°. So, we have the relation
sin(α)/2 = sin(132°)/39.03
α = arcsin(2·sin(132°)/39.03) ≈ 2.18°
The angle below horizontal from the port to the sub is 2.18°.
Part 2
2a. We are given sides 20 and 38 of a triangle and the included angle of 100°. Then the distance (f) from the port to the ship is given by the Law of Cosines as
f² = 20² +38² -2·20·38·cos(100°) ≈ 2107.95
f ≈ 45.91
The distance from port to Ship F is 45.91 km.
2b. The expected treasure location is at a depth that is 2.18° below the horizontal from the port. The tangent ratio for an angle is the ratio of the opposite side (depth) to the adjacent side (distance from F to port), so we have
tan(2.18°) = depth/45.91
depth = 45.91·tan(2.18°) ≈ 1.748
The depth to the expected treasure location is 1.748 km.
2c. The distance from port to the expected treasure location is the hypotenuse of a right triangle. The cosine ratio for an angle is the ratio of the adjacent side to the hypotenuse, so we have
cos(2.18°) = (port to F distance)/(port to treasure distance)
(port to treasure distance) = 45.91 km/cos(2.18°) ≈ 45.95
The distance from the port to the expected treasure is 45.95 km.
Part 3
It seems the Mach 5 Mimi is the ship most likely to have found the treasure. That one seems ripe for attack. Its crew goes to a location that is 2.18° below horizontal. The crew of the FTFF don't have any idea where they are going. (Of course, the pirate ship would have no way of knowing if it is only observing surface behavior.)

5
0