Z score ( X = 1890 ): 1.31
Z score ( X = 1230 ): -0.76
Z score ( X = 2220 ): 2.34 (This value of Z is unusual )
Z score ( X = 1360 ): -0.35
<u>Step-by-step explanation:</u>
Here we have , A standardized exam's scores are normally distributed. In a recent year, the mean test score was 1473 and the standard deviation was 318 . The test scores of four students selected at random are 1890 , 1230 , 2220 , and 1360 . We need to find Find the z-scores that correspond to each value and determine whether any of the values are unusual. Let's find out:
We know that Z score is given by : ( data - Mean ) / ( standard deviation )
Z score ( X = 1890 ):
⇒ 
Z score ( X = 1230 ):
⇒ 
Z score ( X = 2220 ):
⇒ 
This value of Z is unusual as Value lies as : 
.
Z score ( X = 1360 ):
⇒ 
Answer: id say its c
Step-by-step explanation:
Answer:
A. The results were statistically significant.
C. The null hypothesis should be rejected.
Step-by-step explanation:
We are given that a national poll by the Institute for College Access and Success showed that in 69% of college graduates from public and nonprofit colleges in 2013 had student loan debt.
Let p = <em>proportion with student loan debt.
</em>
So, Null Hypothesis,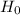 
: p = 69% {means that the proportion of students with graduated with student loan debt equals 69%}
Alternate Hypothesis, 
: p 
69% {means that the proportion with student loan debt does not equal 69%}
The test statistics that would have used here was <u>One-sample z proportion</u> <u>statistics</u>;
We are given the level of significance of 0.05 and P-value of 0.039.
Since, P-value of the test statistics is less than the level of significance as 0.039 < 0.05, <u>so we have sufficient evidence that the results were statistically significant to reject our null hypothesis</u> as it will fall in the rejection region due to which <u>we reject our null hypothesis</u>.
Therefore, we conclude that the proportion with student loan debt does not equal 69%.
Answer:
16 is double 8, so just double the price: 2.64 x 2= $5.28
then, subtract to find the dufference: 5.28 - 4.48= $.80
then, divide that by the oz:
.80/16= 5 cents per ounce
<u>Answer</u>:
5p - 10
<u>Explanation</u>:
total price = (price of each ticket) - $10
<em> let the price of each ticket be p</em>
so equation:
total price = 5p - 10
