Answer:
Step-by-step explanation:
Hello!
1)
<em>To test H0: u= 50 versus H1= u < 50, a random sample size of n = 23 is obtained from a population that is known to be normally distributed. Complete parts A through D. </em>
<em> A) If ¯ x = 47.9 and s=11.9, compute the test statistic .</em>
For thistest the corresponsing statistis is a one sample t-test
B) If the researcher decides to test this hypothesis at the a=0.1 level of significance, determine the critical value(s).
This test is one-tailed to the left, meaning that you'll reject the null hypothesis to small values of the statistic. The ejection region is defined by one critical value:
Check the second attachment. The first row shows α= Level of significance; the First column shows ν= sample size.
The t-table shows the values of the statistic for the right tail. P(tₙ≥α)
But keep in mind that this distribution is centered in zero, meaning that the right and left tails are numerically equal, only the sign changes. Since in this example the rejection region is one-tailed to the left, the critical value is negative.
C) What does the distribution graph appear like?
Attachment.
D) Will the researcher reject the null hypothesis?
As said, the rejection region is one-tailed to the right, so the decision rule is:
If ≤ -1.321, reject the null hypothesis.
If > -1.321, do not reject the null hypothesis.
= -0.85, the decision is to not reject the null hypothesis.
2)
To test H0: μ=100 versus H1:≠100, a simple random sample size of nequals=24 is obtained from a population that is known to be normally distributed. Answer parts (a)-(d).
a) If x =104.2 and s=9.6, compute the test statistic.
For this example you have to use a one sample t-test too. The formula of the statistic is the same:
b) If the researcher decides to test this hypothesis at the α=0.01 level of significance, determine the critical values.
This hypothesis pair leads to a two-tailed rejection region, meaning, you'll reject the null hypothesis at either small or big values of the statistic. Then the rejection region is divided into two and determined by two critical values (the left one will be negative and the right one will be positive but the module of both values will be equal).
c) Draw a t-distribution that depicts the critical region(s). Which of the following graphs shows the critical region(s) in thet-distribution?
Attachment.
(d) Will the researcher reject the null hypothesis?
The decision rule for the two-tailed hypotheses pair is:
If ≤ -2.807 or if
≥ 2.807, reject the null hypothesis.
If -2.807 < < 2.807, do not reject the null hypothesis.
= 2.143 is greater than the right critical value, the decision is to reject the null hypothesis.
Correct option:
B. The researcher will reject the null hypothesis since the test statistic is not between the critical values.
3)
Full text in attachment. The sample size is different by 2 but it should serve as a good example.
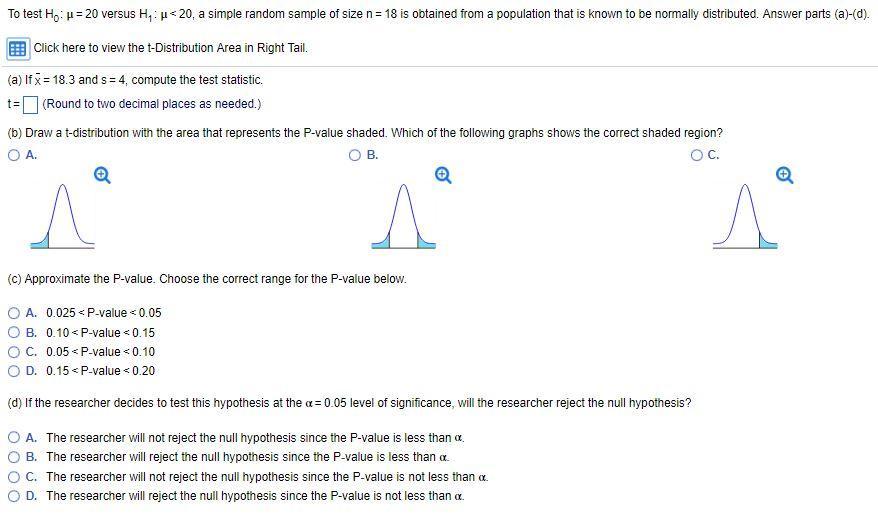
H₀: μ = 20
H₁: μ < 20
a) n= 18, X[bar]= 18.3, S= 4, Compute statistic.
b) The rejection region in this example is one-tailed to the left, meaning that you'll reject the null hypothesis to small values of t.
Out of the three graphics, the correct one is A.
c)
To resolve this you have to look for the values in the t-table that are the closest to the calculated
Symbolically:
= -1.80
Roughly defined you can say that the p-value is the probability of obtaining the value of , symbolically: P(t₁₇≤-1.80)
Under the distribution the calculated statistic is between the values of -2.110 and -1.740, then the p-value will be between their cumulated probabilities:
A. 0.025 < p-value < 0.05
d. The researcher decides to test the hypothesis using a significance level of α: 0.05
Using the p-value approach the decision rule is the following:
If p-value ≤ α, reject the null hypothesis.
If p-value > α, do not reject the null hypothesis.
We already established in item c) that the p-value is less than 0.05, so the decision is to reject the null hypothesis.
Correct option:
B. The researcher will reject the null hypothesis since the p-value is less than α.
I hope this helps!