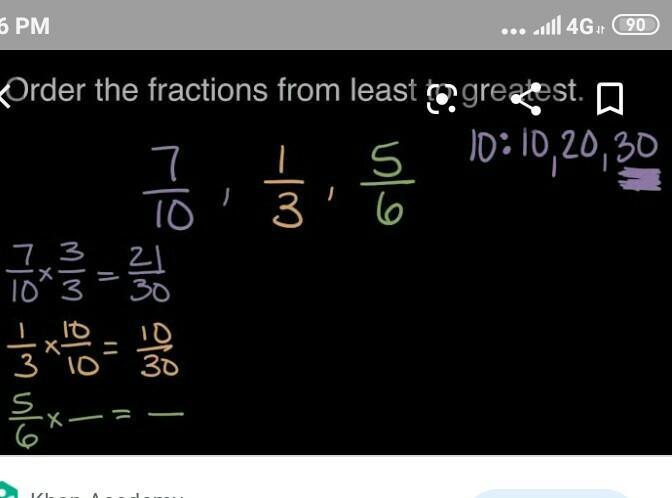
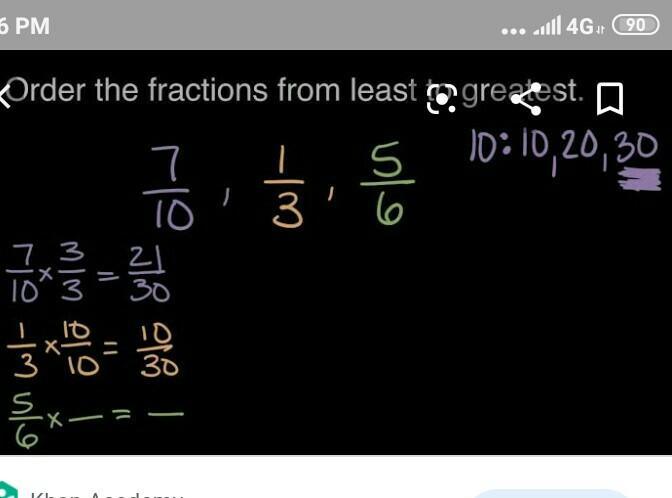
Answer:
Accessibility Links
Skip to main contentAccessibility help
Accessibility feedback
..
To all public transportation workers, thank you
=(x + 6) = 11 copied for free from openupresources.org
About 47,600 results (0.44 seconds)
Ads
Illustrative Math | 6-8 & 9-12 Math Curriculum
Ad·
www.openupresources.org/curriculum
Our Curriculum is Top-Rated on EdReports and Freely Accessible. Learn more today. Interested In Quality Math Curriculum? Request A Quote From Open Up Resources. Supporting Teachers. Professional Learning.
Math CurriculumAbout UsContact UsELA CurriculumSupplemental Materials
Search Results
Web results
Math Curriculum - Open Up Resourcesopenupresources.org › math-curriculum
Open Up Resources 6-8 Math ... Our 6–8 math curriculum is top-rated! ... against acclaimed alignment rubrics (IMET, EQuIP), conducted by leading experts.
Grade 7, Unit 5 - Practice Problems - Open Up Resourcesaccess.openupresources.org › curricula › students › practice_problems
A type of green paint is made by mixing 2 cups of yellow with 3.5 cups of blue. Find a mixture that will make ... A fish starts at -9 meters and changes -11 meters?
Grade 7, Unit 6 - Practice Problems - Open Up Resourcesaccess.openupresources.org › curricula › students › practice_problems
Jada and Priya are trying to solve the equation \frac23+x=4. ... 8 =( -5); 12 ? (-2) = ... 2x = 10; \text-3x = 21; \frac13 x = 6; \text-\frac12x = \text-7 ... Problem 6 (from Unit 4, Lesson 11) ... Jada's teacher fills a travel bag with 5 copies of a textbook.
Missing: free | Must include: free
Open Up Resourcesopenupresources.org
Our nonprofit's mission: to increase equity in education by making excellent, top-rated ... Open Educational Resources (OER) are free to download and use.
Missing: 11 | Must include: 11
Open Up Resources 6–8 Math2nd Edition - Curriculum ...access.openupresources.org › curricula
A problem based curriculum authored by Illustrative Mathematics. This edition of 6–8 Math features enhanced English ... Teacher Family Student. Considering print materials for Open Up Resources 6–8 Mathematics? Request Free Samples ...
Missing: 11 | Must include: 11
Grade 8, Unit 4 - Practice Problems - Open Up Resourcesaccess.openupresources.org › curricula › students › practice_problems
2(\text-3x+4)=5x+2; \text-6x+8=5x+2; 8=11x+2; 6=11x; x=\frac{6}{11} ... Cell phone Plan A costs $70 per month and comes with a free $500 phone. Cell phone ...
Grade 6, Unit 6 - Practice Problems - Open Up Resourcesaccess.openupresources.org › curricula › 6 › students › practice_probl...
Unit 6: Practice Problem Sets. Lesson 1 ... Complete the tape diagram so it represents the equation 5 \boldcdot x = 35. ... Problem 7 (from Unit 3, Lesson 11).
Missing: copied free
Grade 6, Unit 3 - Practice Problems - Open Up Resourcesaccess.openupresources.org › curricula › 6 › students › practice_probl...
How many copies of this flower pattern could you build if you had 30 yellow hexagons, ... She wants to convert 6 quarts to gallons, but cannot decide if she should multiply 6 by 4 or divide 6 by 4 to find her answer. ... Problem 6 (from Unit 2, Lesson 11) ... During a basketball practice, Mai attempted 40 free throws and was ...
Grade 7, Unit 8 - Practice Problems - Open Up Resourcesaccess.openupresources.org › curricula › students › practice_problems
Unit. 1. Lesson 1. What are Scaled Copies? ... An engineer tests the strength of a new material by seeing how much weight it can hold before breaking. Previous tests ... The likelihood that Han makes a free throw in basketball is 60%. ... 5, gggwg. 6, wwggg. 7, gwggg. 8, ggwgw. 9, wwwgg. 10, ggggw. 11, wggwg. 12, gggwg ...
Images for =(x + 6) = 11 copied for free from openupresources.org
Image result for =(x + 6) = 11 copied for free from openupresources.org
Image result for =(x + 6) = 11 copied for free from openupresources.org
Image result for =(x + 6) = 11 copied for free from openupresources.org
Image result for =(x + 6) = 11 copied for free from openupresources.org
Image result for =(x + 6) = 11 copied for free from openupresources.org
Image result for =(x + 6) = 11 copied for free from openupresources.org
Image result for =(x + 6) = 11 copied for free from openupresources.org
Image result for =(x + 6) = 11 copied for free from openupresources.org
Image result for =(x + 6) = 11 copied for free from openupresources.org
Image result for =(x + 6) = 11 copied for free from openupresources.org
View all
More images for =(x + 6) = 11 copied for free from openupresources.org
Report images
Page Navigation
1
2
3
4
5
6
7
8
9
10
Next
Footer Links
Step-by-step explanation: