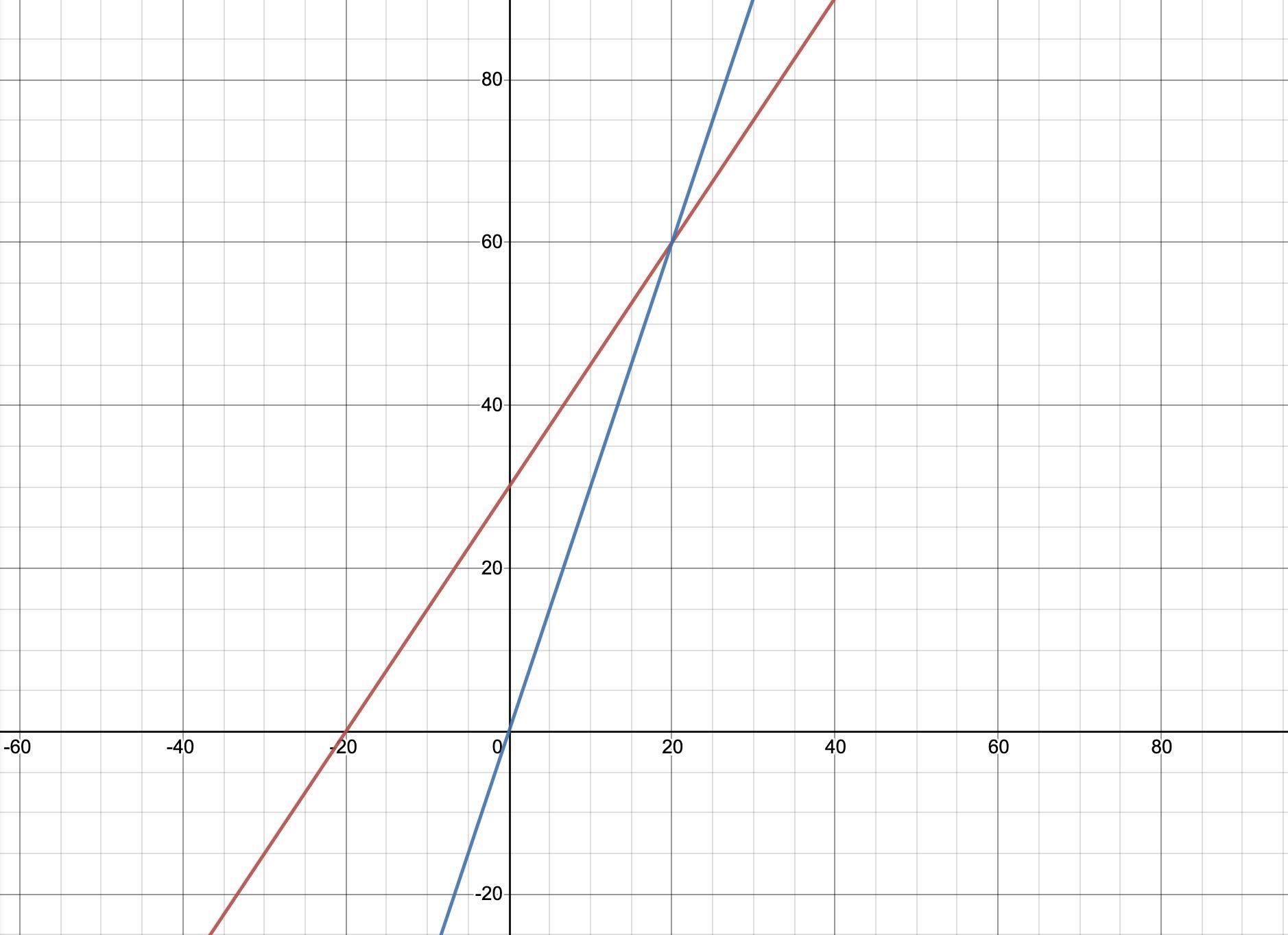
Answer:
A) Carla: y = 1.5x + 30 <-- y is the total money, and x is the number of weeks
Darla: y = 3x <-- y is the total money, and x is the number of weeks
B) No, they start with a different amount of money and also save different amounts each week. They will not always have the same amount of money.
C) See attachment
Step-by-step explanation:
We'll start with Carla.
Carla saves $1.5 every week. That means that if we multiply the number of weeks she has saved by 1.5 we'll get the amount of money she has. However, she starts at 30 so we have to add 30 to that at the beginning. So, Carla's equation is y = 1.5x + 30. y is the total money, and x is the number of weeks
Darla saves $3 every week. That means that if we multiply the number of weeks she has saved by 3 we'll get the amount of money she has. Unlike Carla, Darla starts at $0, so there is no need to add anything. So, Darla's equation is y = 3x. y is the total money, and x is the number of weeks
Since Carla and Darla start with a different amount of money and save different amounts each week, they won't always have the same amount of money. However, they will cross at some point. You can actually see this in the graph. Carla, there is red, and Darla is blue.
Now let's graph the 2 equations. First, we'll do Carla. her equation is y = 1.5x + 30. Since it is in the slope-intercept form we can just use y = mx + b to tell how we're going to graph this. In this formula, m is the slope, and b is the y-intercept. As you can see when you look back at Carla's equation, m is 1.5 and b is 30. First, we'll take the y-intercept, b, which is 30 as we just figured out, and plot it on the graph. All you have to do here is count 30 units up the y-axis (the one going up and down) and put a point there. Now we take the slope (1.5) and we start putting in points that the line will go through. 1.5 in fraction form is 3/2 meaning (starting from that point we marked earlier) we will go 3 units up, and 2 units to the right and put another point there. You can now take a ruler, line up the 2 points you marked and draw a big line through them that keeps going on forever on both sides (just put an arrow at both ends to mark that).
Now we'll do the same with Darla's equation. Her's is y = 3x. When we compare this with or slope-intercept formula, y = mx + b, we'll notice there is no b. That means it is 0 and that the y-intercept is also 0. So go ahead and mark a point in the middle of the graph where the 2 big lines cross. 3 in fraction form is just 3/1 meaning that we'll go 3 up and 1 to right (from the point you just marked) and put another point there. Now draw another big line through both of those points (WITH A RULER) and mark the ends with arrows.