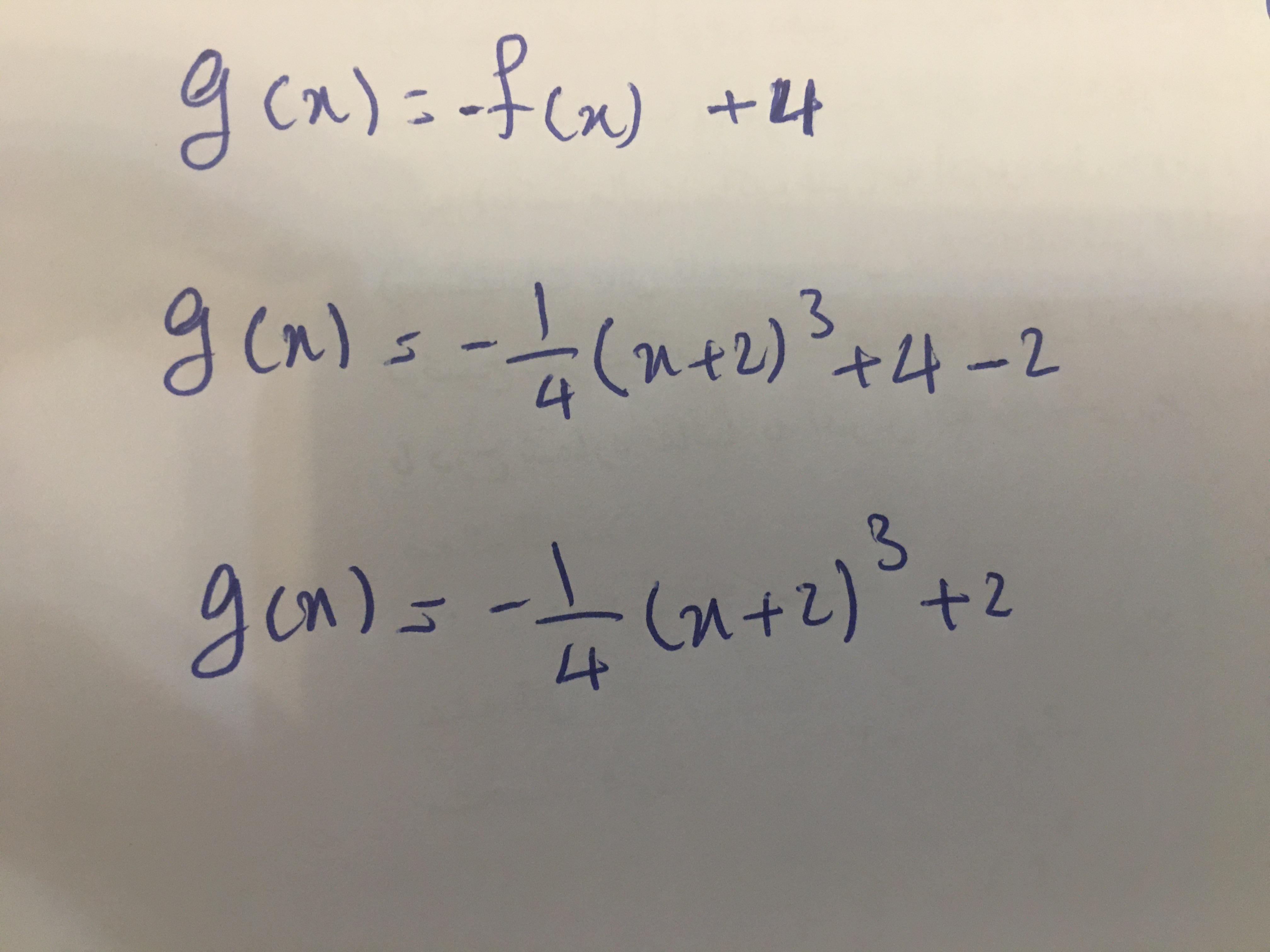Answer:
Rearrange:
Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation :
7/n-(8/7)=0
Step by step solution :
STEP 1:
8
Simplify —
7
The equation at the end of step
1:
7 8
— - — = 0
n 7
STEP 2:
7
Simplify —
n
The equation at the end of step
2:
7 8
— - — = 0
n 7
STEP 3:
Calculating the Least Common Multiple :
3.1 Find the Least Common Multiple
The left denominator is : n
The right denominator is : 7
Number of times each prime factor
appears in the factorization of:
Prime
Factor Left
Denominator Right
Denominator L.C.M = Max
{Left,Right}
7 0 1 1
Product of all
Prime Factors 1 7 7
Number of times each Algebraic Factor
appears in the factorization of:
Algebraic
Factor Left
Denominator Right
Denominator L.C.M = Max
{Left,Right}
n 1 0 1
Least Common Multiple:
7n
Calculating Multipliers :
3.2 Calculate multipliers for the two fractions
Denote the Least Common Multiple by L.C.M
Denote the Left Multiplier by Left_M
Denote the Right Multiplier by Right_M
Denote the Left Denominator by L_Deno
Denote the Right Multiplier by R_Deno
Left_M = L.C.M / L_Deno = 7
Right_M = L.C.M / R_Deno = n
Making Equivalent Fractions :
3.3 Rewrite the two fractions into equivalent fractions
Two fractions are called equivalent if they have the same numeric value.
For example : 1/2 and 2/4 are equivalent, y/(y+1)2 and (y2+y)/(y+1)3 are equivalent as well.
To calculate equivalent fraction, multiply the numerator of each fraction, by its respective Multiplier.
L. Mult. • L. Num. 7 • 7
—————————————————— = —————
L.C.M 7n
R. Mult. • R. Num. 8 • n
—————————————————— = —————
L.C.M 7n
Adding fractions that have a common denominator :
3.4 Adding up the two equivalent fractions
Add the two equivalent fractions which now have a common denominator
Combine the numerators together, put the sum or difference over the common denominator then reduce to lowest terms if possible:
7 • 7 - (8 • n) 49 - 8n
——————————————— = ———————
7n 7n
The equation at the end of step
3
:
49 - 8n
——————— = 0
7n
STEP
4
:
When a fraction equals zero :
4.1 When a fraction equals zero ...
Where a fraction equals zero, its numerator, the part which is above the fraction line, must equal zero.
Now, to get rid of the denominator, Tiger multiplies both sides of the equation by the denominator.
Here's how:
49-8n
————— • 7n = 0 • 7n
7n
Now, on the left-hand side, the 7n cancels out the denominator, while, on the right-hand side, zero times anything is still zero.
The equation now takes the shape :
49-8n = 0
Solving a Single Variable Equation:
4.2 Solve : -8n+49 = 0
Subtract 49 from both sides of the equation :
-8n = -49
Multiply both sides of the equation by (-1) : 8n = 49
Divide both sides of the equation by 8:
n = 49/8 = 6.125
One solution was found :
n = 49/8 = 6.125
Step-by-step explanation:
hope this helps...