Match the number of the solution to the letter of the problem to learn the name of one of the greatest mathematical minds who ev
1 answer:
You might be interested in
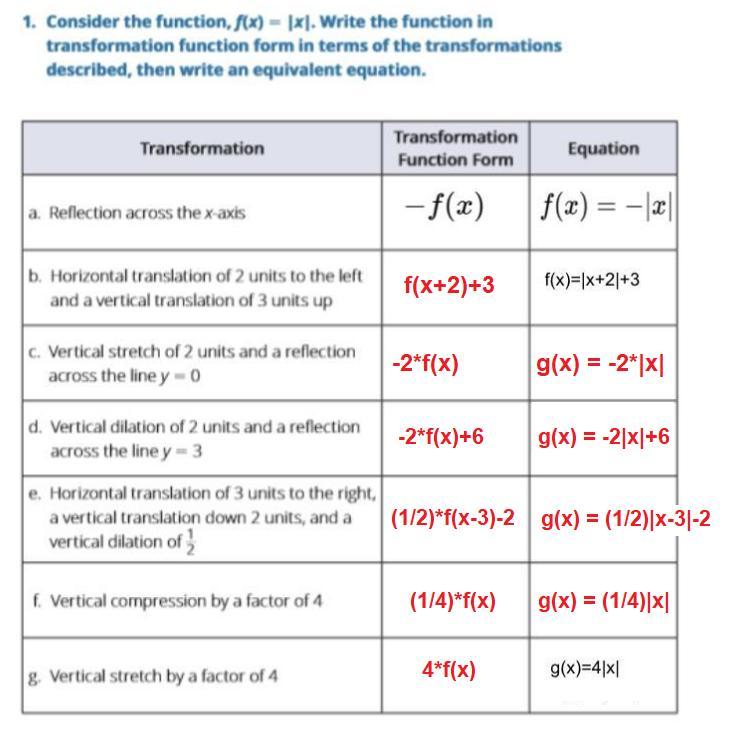
Answer: Check out the attached diagram below for the filled out table.
Explanation:
- A) This is correct. You basically stick a minus sign out front to reflect over the x axis (aka the line y = 0).
- B) Replacing x with x+2 will shift the graph 2 units to the left. Adding on 3 at the end will shift it up 3 units.
- C) A vertical stretch, aka vertical dilation, makes the graph taller than it already is. In this case, we want to stretch it to make it twice as tall. That explains the 2 out front. The negative is there to reflect over the x axis.
- D) The -2 is to apply a dilation of 2 and do a reflection. The +6 is so ensure that the vertex arrives at the proper location (0,6) so that we reflect over y = 3.
- E) This is similar to part B. Replacing x with x-3 shifts the graph 3 units to the right. We subtract off 2 at the end to shift the graph down 2 units. The 1/2 out front applies the dilation, which in this case is a vertical compression by a factor of 2.
- F) A vertical compression by a factor of 4 is the same as dilating by a factor of 1/4. So we'll multiply f(x) by 1/4.
- G) Similar to part F, but we'll be using the scale factor 4 this time.
Answer: 0.0898
Step-by-step explanation:
Probability =
Given : Sample size : 528
Number pf customers say they are happy = 237
Probability of getting one happy customer=
Probability of getting second happy customer= [subtract 1 from both numbers]
Probability of getting third happy customer=
If 3 customers are elected without replacement
The probability they will all say they are happy with the service =
Hence, the required probability = 0.0898