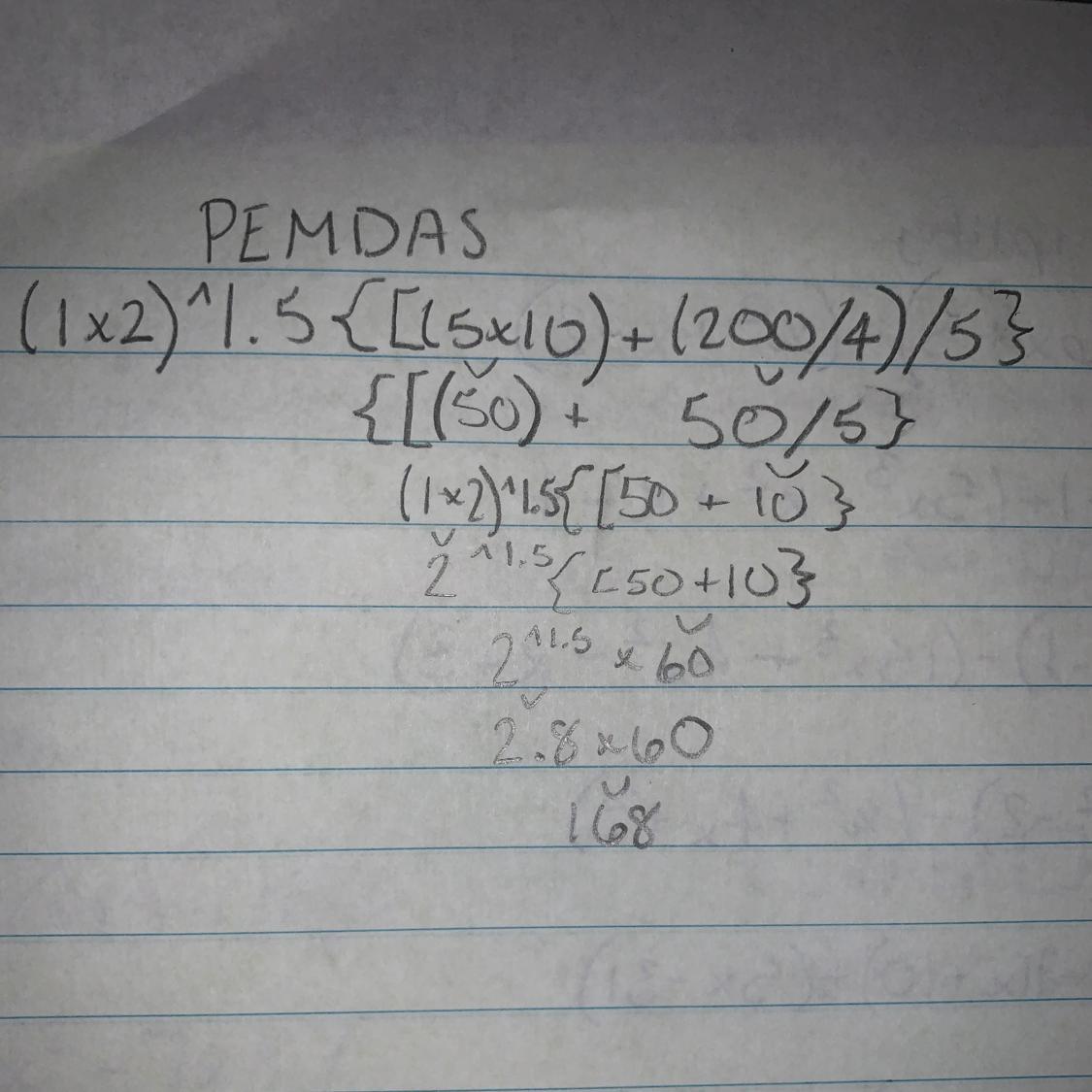Answer: The correct answer is: [A]:
__________________________________________________
" Look at the graph of the relationship. Find the y-value of the point that corresponds to x = 1 . That value is the unit rate. "
__________________________________________________
Step-by-step explanation:
__________________________________________________
Note that the "unit rate" is the term that refers to:
a "quantity" / or "quantitative value" ;
→ of some type of "countable units"
{e.g. "currency" — [such as: dollars, cents, pounds] ; "distance/length/ width/ height" — [such as: miles, kilometers, meters, centimeters, yards, feet, inches] ; pieces of fruits — [such as: number of apples; cans of soda, number of red dresses] ;
__________________________________________________
per "single unit" of something — {e.g. per hour; per minute; per mile; per ounce; per hour; per dollar, per kilometer, per day, per week.
{e.g.
→ " 3 apples eaten per [single] apricot eaten" ;
→ " 46 miles per hour.
→ " 8.3 cents per oz." ;
→ " 5 Liters of soda per dollar " ;
→ " 2.3 grams per mole " ;
→ " 4.6 mg solute / kg of solvent " ;
→ " 5 km / hr " ; {that is: " 5 km per hr " } .
→ " 3 yds. per [single] square inch."
→ " 35 parts per hundred" ; {that is: " 35 percent" ; or: " 35 % " . } .
→ " ... The cilantro is on sale for 33 cents per bundle ...} ."
→ ... to provide a few examples.
__________________________________________________
On on Cartesian plane graph, the "x-axis" is located on the "horizontal axis" that represents the "independent variable" (or, at times, the "experimental value" — which can be manipulated — or "controlled" —or be subjected to being "manipulated" / "controlled" / or, "selected".
The "y-axis" is located on the "vertical axis" that represents the "dependent variable" (or, at times, the "control value") that cannot be "manipulated" / controlled/ or "selected" / since it represents the "y-value" of the corresponding coordinate to which the "x-value" happens to corresponds to at the given value for "x" .
So, if the "unit rate" represents the "single unit rate" ; we look at "x = 1 " ; since we are "choosing" this particular "single" rate of per "single" (i.e. "1" ) ; so we do not have a choice in what "y-value" of the particular graph to select. We can control the fact that we are "choosing" to find the "unit" rate, so we select the "independent variable" , "x = 1 " . We then examine the "corresponding y-value" that happens to exist when "x = 1 " .
{Note that we have "no control" over what that "y-value" is ; at the: "[point which: " x = 1 .] . "
_________________________________________________
→ As such, that "y-value" [insert that numeric "y-value" ; followed by the units represented by the "y-axis" ] ;
per " 1 " [insert "single unit" represented by the "x-axis" ] ;
_________________________________________________
→ is the: "unit rate" .
__________________________________________________
So:
The correct answer is: [A]:
__________________________________________________
" Look at the graph of the relationship. Find the y-value of the point that corresponds to x = 1 . That value is the unit rate. "
__________________________________________________
Hope this answer is helpful to you!
Best wishes to you in your academic endeavors —
and within the "Brainly" community!
__________________________________________________