Even function:
A function is said to be even if its graph is symmetric with respect to the , that is:
Odd function:
A function is said to be odd if its graph is symmetric with respect to the origin, that is:
So let's analyze each question for each type of functions using examples of polynomial functions. Thus:
FOR EVEN FUNCTIONS:
1. When becomes
1.1 Effects on the y-intercept
We need to find out the effects on the y-intercept when shifting the function into:
We know that the graph intersects the y-axis when , therefore:
So:
So the y-intercept of is one unit less than the y-intercept of
1.2. Effects on the regions where the graph is increasing and decreasing
Given that you are shifting the graph downward on the y-axis, there is no any effect on the intervals of the domain. The function increases and decreases in the same intervals of
1.3 The end behavior when the following changes are made.
The function is shifted one unit downward, so each point of has the same x-coordinate but the output is one unit less than the output of . Thus, each point will be sketched as:
FOR ODD FUNCTIONS:
2. When becomes
2.1 Effects on the y-intercept
In this case happens the same as in the previous case. The new y-intercept is one unit less. So the graph is shifted one unit downward again.
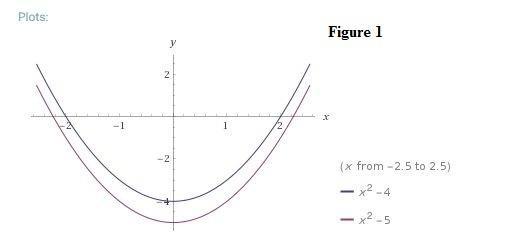
An example is shown in Figure 1. The graph in blue is the function:
and the function in red is:
So you can see that:
2.2. Effects on the regions where the graph is increasing and decreasing
The effects are the same just as in the previous case. So the new function increases and decreases in the same intervals of
In Figure 1 you can see that both functions increase at:
and decrease at:
2.3 The end behavior when the following changes are made.
It happens the same, the output is one unit less than the output of . So, you can write the points just as they were written before.
So you can realize this concept by taking a point with the same x-coordinate of both graphs in Figure 1.
FOR EVEN FUNCTIONS:
3. When becomes
3.1 Effects on the y-intercept
We need to find out the effects on the y-intercept when shifting the function into:
As we know, the graph intersects the y-axis when , therefore:
And:
So the new y-intercept is the negative of the previous intercept shifted one unit upward.
3.2. Effects on the regions where the graph is increasing and decreasing
In the intervals when the function increases, the function decreases. On the other hand, in the intervals when the function decreases, the function increases.
3.3 The end behavior when the following changes are made.
Each point of the function has the same x-coordinate just as the function and the y-coordinate is the negative of the previous coordinate shifted one unit upward, that is:
FOR ODD FUNCTIONS:
4. When becomes
4.1 Effects on the y-intercept
In this case happens the same as in the previous case. The new y-intercept is the negative of the previous intercept shifted one unit upward.
4.2. Effects on the regions where the graph is increasing and decreasing
In this case it happens the same. So in the intervals when the function increases, the function decreases. On the other hand, in the intervals when the function decreases, the function increases.
4.3 The end behavior when the following changes are made.
Similarly, each point of the function has the same x-coordinate just as the function and the y-coordinate is the negative of the previous coordinate shifted one unit upward.