All categories

4 years ago

Does anyone know this answer to this questions

Mathematics

1 answer:

7nadin3 [17]4 years ago

4 0

ANSWER

-4.0

EXPLANATION

The given trigonometric equation is

$\tan \: 45 \degree - 10 \: \cos \: 60 \degree$

From special angles or using the unit circle.

$\tan \: 45 \degree = 1$

$\cos \: 60 \degree = \frac{1}{2}$

We make the substitution to get:

$1 - 10 ( \frac{1}{2} ))$

This simplifies to:

$1 - 5 = - 4$

Hence the correct answer is -4.0

You might be interested in

Which best describes two figures that are similar?

mina [271]

Answer:

Step-by-step explanation:

3 0

3 years ago

An entrepreneur is considering the purchase of a coin-operated laundry. The current owner claims that over the past 5 years, the

notsponge [240]

Answer:

We conclude that the daily average revenue was actually $675.

Step-by-step explanation:

We are given that the current owner claims that over the past 5 years, the average daily revenue was $675 with a standard deviation of $75.

A sample of 30 days reveals a daily average revenue of $625.

Let $\mu$ = daily average revenue.

So, Null Hypothesis, 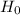$H_0$ : $\mu$ = $675 {means that the daily average revenue was $675}

Alternate Hypothesis, $H_A$ : $\mu$ $\neq$ $675 {means that the daily average revenue was different from $675}

The test statistics that would be used here One-sample z test statistics as we know about the population standard deviation;

T.S. = $\frac{\bar X-\mu}{\frac{\sigma}{\sqrt{n} } }$ ~ N(0,1)

where, $\bar X$ = sample daily average revenue = $625

$\sigma$ = population standard deviation = $75

n = sample of days = 30

Since, we are given that we have decided not to reject the null hypothesis which leads us to the conclusion that the daily average revenue was actually $675.

3 0

4 years ago

How do you round 60.95 to the nearest whole number ? What will it become

Nuetrik [128]

It will become 61
because anything above 0.5 rounds up

5 0

3 years ago

Read 2 more answers

Evaluate the expression when x=1/3 and y=-7/4 3x+y

dolphi86 [110]

Answer) -3/4 or decimal form -0.75

4 0

3 years ago

Read 2 more answers

If BC = 6.5, CD = 7.8, and AD = 12.2, find AB to the nearest tenth.

Sladkaya [172]

This can be solved using the angle bisector theorem. Note that line segment AD is the angle bisector of triangle DAB from angle DAB. Therefore, we know that the ratios $\frac{\text{AD}}{\text{CD}}$ and $\frac{\text{AB}}{\text{CB}}$ are equal. Solving, we get $\frac{\text{12.2}}{\text{7.8}}=\frac{\text{AB}}{\text{6.5}}$ . Cross multiplying, we get $79.3 = 7.8x$ , and solving this equation we get $x = 10.1666... \approx 10.2$ . 10.2 is your answer.

6 0

4 years ago