1. First we are going to find the vertex of the quadratic function 
. To do it, we are going to use the vertex formula. For a quadratic function of the form 
, its vertex 
is given by the formula 
; 
.
We can infer from our problem that
and 
, sol lets replace the values in our formula:
Now, to find
, we are going to evaluate the function at 
. In other words, we are going to replace 
with -2 in the function:
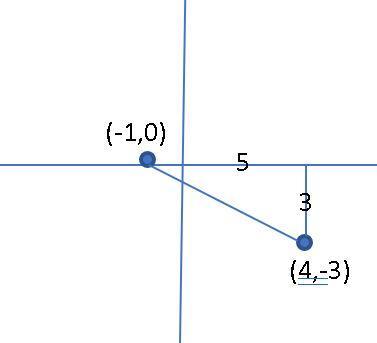
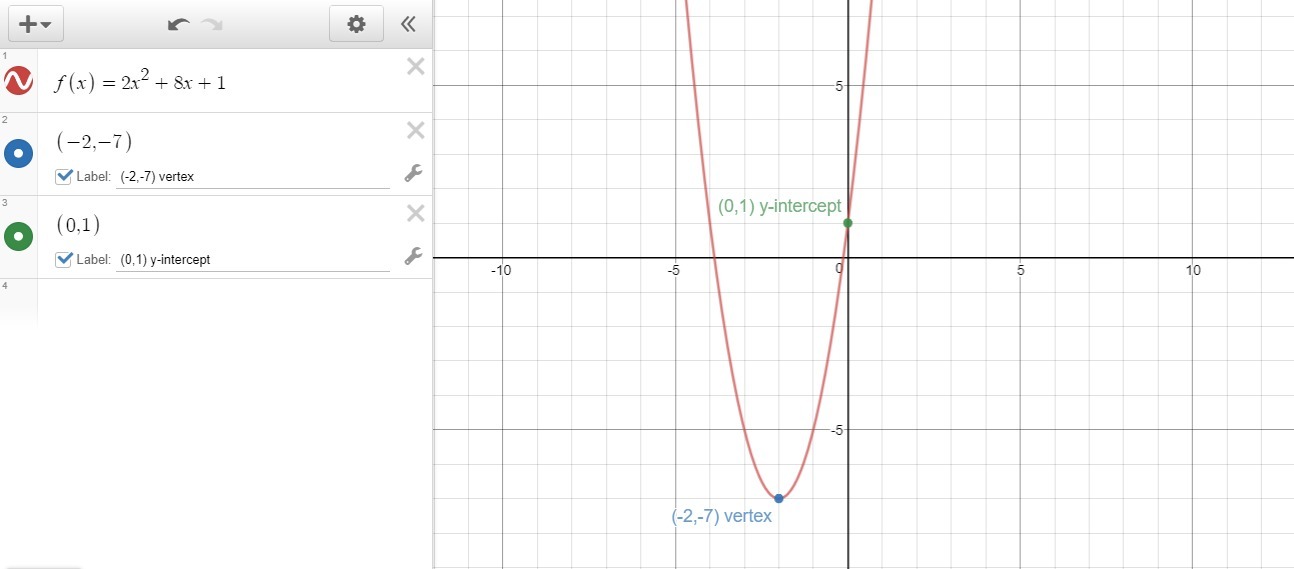
So, our first point, the vertex of the parabola, is the point 
.
To find our second point, we are going to find the y-intercept of the parabola. To do it we are going to evaluate the function at zero; in other words, we are going to replace with 0:
So, our second point, the y-intercept of the parabola, is the point (0,1)
We can conclude that using the vertex (-2,-7) and a second point we can graph as shown in picture 1.
2. The vertex form of a quadratic function is given by the formula:
where
is the vertex of the parabola.
We know from our previous point how to find the vertex of a parabola. and , so lets find the vertex of the parabola 
.
Now we can use our formula to convert the quadratic function to vertex form:
We can conclude that the vertex form of the quadratic function is.
3. Remember that the x-intercepts of a quadratic function are the zeros of the function. To find the zeros of a quadratic function, we just need to set the function equal to zero (replace
with zero) and solve for .
To solve for, we need to factor our quadratic first. To do it, we are going to find two numbers that not only add up to be equal 4 but also multiply to be equal -60; those numbers are -6 and 10.
Now, to find the zeros, we just need to set each factor equal to zero and solve for.
and 
and 
We can conclude that the x-intercepts of the quadratic function are the points (0,6) and (0,-10).
4. To solve this, we are going to use function transformations and/or a graphic utility.
Function transformations.
- Translations:
We can move the graph of the function up or down by adding a constant
to the y-value. If 
, the graph moves up; if 
, the graph moves down.
- We can move the graph of the function left or right by adding a constant to the x-value. If , the graph moves left; if , the graph moves right.
- Stretch and compression:
We can stretch or compress in the y-direction by multiplying the function by a constant. If 
, we compress the graph of the function in the y-direction; if 
, we stretch the graph of the function in the y-direction.
We can stretch or compress in the x-direction by multiplying by a constant . If , we compress the graph of the function in the x-direction; if , we stretch the graph of the function in the x-direction.
a. The value of is 2; the value of 
is -3. Since is added to the whole function (y-value), we have an up/down translation. To find the translation we are going to ask ourselves how much should we subtract to 2 to get -3?
Since, we can conclude that the correct answer is: It is translated down 5 units.
b. Using a graphing utility to plot both functions (picture 2), we realize that is 1 unit to the left of
We can conclude that the correct answer is: It is translated left 1 unit.
c. Here we have that is multiplied by the constant term 2. Remember that We can stretch or compress in the y-direction (vertically) by multiplying the function by a constant .
Since, we can conclude that the correct answer is: It is stretched vertically by a factor of 2.
We can infer from our problem that
Now, to find
So, our first point, the vertex
To find our second point, we are going to find the y-intercept of the parabola. To do it we are going to evaluate the function at zero; in other words, we are going to replace
So, our second point, the y-intercept of the parabola, is the point (0,1)
We can conclude that using the vertex (-2,-7) and a second point we can graph
2. The vertex form of a quadratic function is given by the formula:
where
We know from our previous point how to find the vertex of a parabola.
Now we can use our formula to convert the quadratic function to vertex form:
We can conclude that the vertex form of the quadratic function is
3. Remember that the x-intercepts of a quadratic function are the zeros of the function. To find the zeros of a quadratic function, we just need to set the function equal to zero (replace
To solve for
Now, to find the zeros, we just need to set each factor equal to zero and solve for
We can conclude that the x-intercepts of the quadratic function
4. To solve this, we are going to use function transformations and/or a graphic utility.
Function transformations.
- Translations:
We can move the graph of the function up or down by adding a constant
- We can move the graph of the function left or right by adding a constant
- Stretch and compression:
We can stretch or compress in the y-direction by multiplying the function by a constant
We can stretch or compress in the x-direction by multiplying
a. The
Since
b. Using a graphing utility to plot both functions (picture 2), we realize that
We can conclude that the correct answer is: It is translated left 1 unit.
c. Here we have that
Since