For this answer let's pick the Fish Pond.
QUESTION: <span>What do you know?
We know that the total area of the rectangular patio is 24 square feet. The rectangular fish pond that we want to build should have the length that is twice the width. We also need a 1-foot border around the pond.
The total area of the patio is represented by </span> where x is the width of the fish pond.
where x is the width of the fish pond.
QUESTION: What do you want to find out?
We can answer this question by examining what we have been given (we have answered this in the previous question). Since we only have one variable in the equation and this is the width of the fish pond, then this is the only thing that we need to find out. The length will just follow after the width is solved. (Basically, we are concerned with the dimensions of our project.)
QUESTION: What kind of answer do you expect?
Since we are only expecting to solve for the dimensions, then we should expect two numbers which would represent the width and the length. Through the polynomial, we can get the width of our project, then the length would just be twice our answer for the width.
1. To set our polynomial equation equal to the total area of our patio, we just write the equation on the left side and the total area of the patio on the right. We recall the equation that we gave in the first question above as well as the patio's area.

2. For this item, we just simply negate the constant term on the right side by subtracting the same number to both sides. Since our constant term is 24, we subtract 24 from the polynomial as well as the term on the right side.


3. In this item we are only tasked to find the GCF of the trinomial and factor it out of the left side of the equation. The GCF just means the common number or variable in all terms. Upon examining, we can see that the only common factor of the terms is 2 (since all terms are divisible by 2), thus this will be the GCF and we will factor this one out.

4. To factor the polynomial completely, we just figure out the possible factors of the quadratic equation. You can do this by trying out all factors of -10 that will have a sum of 3 (since -10 is the constant and 3 is the coefficient of x). Upon examining you should end up with:
 (Notice that 5 and -2 are factors of -10 and their sum is 3).
(Notice that 5 and -2 are factors of -10 and their sum is 3).
5. The rule stated on this item just means that we can equate each individual factor to zero (except for the constant term) to find out the possible values of x. That means that we can solve for x by using the equations x+5=0 and x-2=0.




6. For this item, we just do simple substitutions to the equation to verify whether the values we got in question 5 is really a solution to the equation. The values of x that we got are -5 and 2 so we substitute these one at a time.
to verify whether the values we got in question 5 is really a solution to the equation. The values of x that we got are -5 and 2 so we substitute these one at a time.






Both values of x make the left side equal to zero therefore both are solutions to the equation.
7. We can tell the dimensions of the project by looking at the values that we got for x, since we assumed x to be the width of our project. The fact that we got two values for x won't be a problem since one of these values is negative. There is no negative measurement/width so we can just ignore this negative value (-5). Thus, the width for our project would be 2 and the length would be twice this value which is 4.
Width = 2 feet
Length = 4 feet
8. For this item, we just illustrate the dimensions of our project and add a 1-foot border (as we are told initially). You can see this illustration in the picture I attached below.
Since we have an extra 1 foot in every side, that means we need to add 2 feet to both the width and the length. Therefore, our width now is 4 while our length is 6.
Multiplying these numbers to verify the area, we get 24 square feet which is exactly the area of the patio.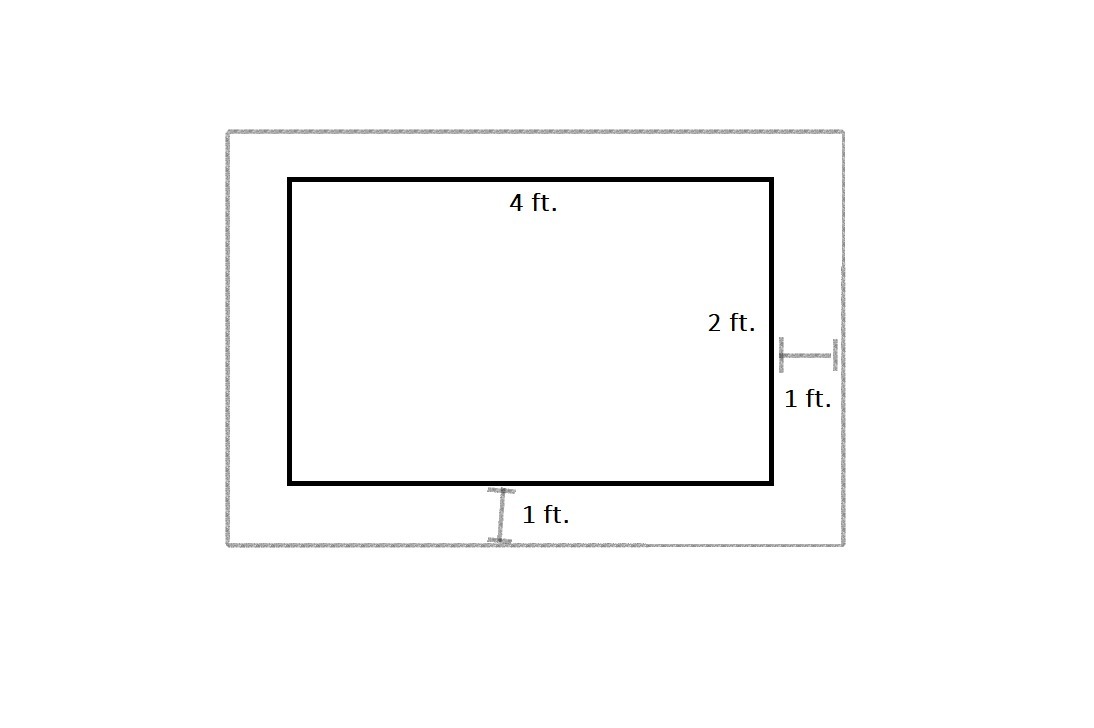
QUESTION: <span>What do you know?
We know that the total area of the rectangular patio is 24 square feet. The rectangular fish pond that we want to build should have the length that is twice the width. We also need a 1-foot border around the pond.
The total area of the patio is represented by </span>
QUESTION: What do you want to find out?
We can answer this question by examining what we have been given (we have answered this in the previous question). Since we only have one variable in the equation and this is the width of the fish pond, then this is the only thing that we need to find out. The length will just follow after the width is solved. (Basically, we are concerned with the dimensions of our project.)
QUESTION: What kind of answer do you expect?
Since we are only expecting to solve for the dimensions, then we should expect two numbers which would represent the width and the length. Through the polynomial, we can get the width of our project, then the length would just be twice our answer for the width.
1. To set our polynomial equation equal to the total area of our patio, we just write the equation on the left side and the total area of the patio on the right. We recall the equation that we gave in the first question above as well as the patio's area.
2. For this item, we just simply negate the constant term on the right side by subtracting the same number to both sides. Since our constant term is 24, we subtract 24 from the polynomial as well as the term on the right side.
3. In this item we are only tasked to find the GCF of the trinomial and factor it out of the left side of the equation. The GCF just means the common number or variable in all terms. Upon examining, we can see that the only common factor of the terms is 2 (since all terms are divisible by 2), thus this will be the GCF and we will factor this one out.
4. To factor the polynomial completely, we just figure out the possible factors of the quadratic equation. You can do this by trying out all factors of -10 that will have a sum of 3 (since -10 is the constant and 3 is the coefficient of x). Upon examining you should end up with:
5. The rule stated on this item just means that we can equate each individual factor to zero (except for the constant term) to find out the possible values of x. That means that we can solve for x by using the equations x+5=0 and x-2=0.
6. For this item, we just do simple substitutions to the equation
Both values of x make the left side equal to zero therefore both are solutions to the equation.
7. We can tell the dimensions of the project by looking at the values that we got for x, since we assumed x to be the width of our project. The fact that we got two values for x won't be a problem since one of these values is negative. There is no negative measurement/width so we can just ignore this negative value (-5). Thus, the width for our project would be 2 and the length would be twice this value which is 4.
Width = 2 feet
Length = 4 feet
8. For this item, we just illustrate the dimensions of our project and add a 1-foot border (as we are told initially). You can see this illustration in the picture I attached below.
Since we have an extra 1 foot in every side, that means we need to add 2 feet to both the width and the length. Therefore, our width now is 4 while our length is 6.
Multiplying these numbers to verify the area, we get 24 square feet which is exactly the area of the patio.

6
0