Answer:
Option (A) is the correct answer to this question.
Explanation:
The cessation of the Sporty line would forfeit the profits produced by the Sporty line business, but the business (Beautiful Watches) will have to bear the $38,000 fixed expenses involved by Spotify Watches.
However, if production continued, the Sporty watches would have suffered a loss of $32,000. The company will bear fixed costs regardless of whether the company continues or discontinues the Sporty line market.
Accordingly, the gross operating profits should have been
= Total operating expenses - ( $ 38000 - $ 32000)
= $ 55000 - ( $ 38000 - $ 32000)
= $ 55000 - $ 6000
= $ 49000
There is also a fall of $6000 ($55000-$49000) in operating profits.
Other options are incorrect because they are not related to the given scenario.
Answer:
D. debit card
Explanation:
A debit card is an electronic card that enables customers to access their bank accounts via an ATM. An ATM ( Automated Teller Machine) is a banking outlet that allows customers to perform basic banking services such as deposits, withdrawals, transfers, and balance inquiries without stepping into the banking hall.
A customer needs to have their debit card and the PIN to access their bank account via the ATM.
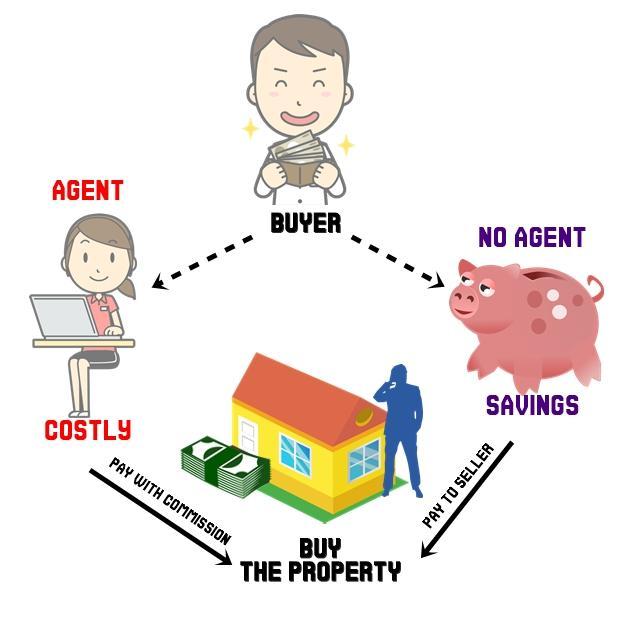
"The use of a buyer's agent guarantees that the buyer will get a property for the lowest price possible" is NOT an advantage of buyer's agency.
It is true that the efforts that a buyer's agent exerts on behalf of the buyer cannot be compromised and that the buyers can freely communicate confidential information without fear that disclosing that information will weaken their negotiating position. The buyers will also have the benefit of a licensee's expertise in finding the right property, negotiating the purchase and attending to closing details.
However, using a buyer's agent won't guarantee that the buyer can get the best deal on a property; as a result, this is not one of the advantages of buyer's agency. The agent would only consider what is best for the buyer and not the cheapest.
Agents will also charge extra fees and commissions for representing their buyers. To avoid additional expenses, some buyers and sellers choose not to use an agent. In order to save more money and find a property for the lowest price, buyers should avoid using an agent and instead deal directly with the seller.
Learn what happens when there's no buyer agency agreement in place here: brainly.com/question/28066390
#SPJ4
Answer:
options-based planning.
Explanation:
Options-based planning is a strategy that guards against failure. The business makes small Investments in several alternative plans. It considers what could go wrong in business operations and plans alternative measures to mitigate total failure.
Woolplanknis an apparel company, and to protect against failure they invested in 5 sheep farms. This year they are planning to nlbuy the most profitable sheep farm. They are using options based planning.
Answer:
A) operant conditioning
Explanation:
Operant conditioning is a method that operates on either reward or punishment of employees behavior and attitude towards the job.
From the companies policy initiative it has created a pay-as-you-work environment for the employees ( i.e. "the more you work the more you get paid" - Reward and "the less you work the less you get paid" - Punishment )