Answer:
Modify (restrict) the function's Domain as indicated below
Step-by-step explanation:
The factory would study the expenses involved with setting the factory into production, wages for workers' salaries, and other factory running expenses into the total cost of producing the units (such would obviously drastically change the graph from the one presented), and make sure that there is a threshold at least on the "breaking even" with the estimated revenue coming from the units produced/ordered.
That threshold can be set to a "<em>minimal</em>" number of units ordered in order to start production. If one wants to use the original graph, with some minor modifications, one can change it so it starts from that threshold point onward. For example, if the minimal number of units to be produced in order to "break even" considering the "revenue minus total expenses larger than zero" condition, the given graph could be modified to the one shown in red in the image attached. In such graph we are estimating that the positive "revenue minus total cost" break even point is at the production of 13,000 units, so we set the starting of the piece-wise function there, and use a non-solid dot to indicate that the number of units produce should be strictly larger than the break-even point (13,000 units) in order to be profitable. This involves a change in the original function's Domain, restricting its first section from the original one (which starts at zero: 
) to a domain that starts at a number of units strictly larger than 13,000 (
) in our example
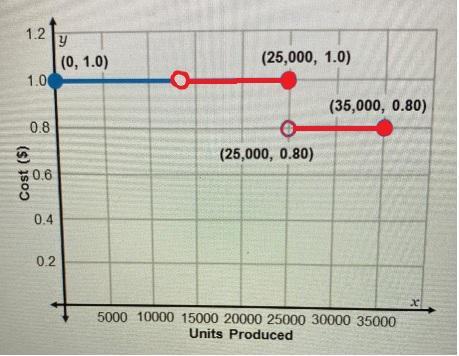
Answer:
A. (2,5)
Step-by-step explanation:
Answer:
D 2i
Step-by-step explanation:
Answer:
Scott will have to do 44 practices
Step-by-step explanation:
Let X be the number of yards per practice.
Let P = number of practice Scott needs to do.
Multiply 20 yards by 4 sprints
X = 20yards × 4 sprints = 80 yards
Number of yards he had to sprint per practice will be:
1 mile = 1760 yards
Converting from miles to yards
X = 1760 × 2 miles = 3520 yards
Number of practice,P Scott need to do = (3520/80)yards
Number of Practice,P = 44
I think you're asking for a numerical answer, but you didn't mention
your score on the final.
Since the final is worth 10% (one tenth) of the grade, that 71 that you
have going into the final is worth 9/10 of the grade. So the way you
calculate your overall average is
Overall score = 1/10 of [ (71 x 9) + score on the final ] .
If you scored absolute zero on the final, your overall average would be
Overall score = (1/10) x [ (71 x 9) + 0 ] = (1/10) (639) = <u>63.9%</u> .
That's the lowest overall score for the class that you can have.
The <u>highest</u> overall score you could have would be if you got 100% on the final.
Then
Overall = (1/10) x (639 + 100) = (1/10) x (739) = <u>73.9%</u> .
If you got a 50% on the final, your overall would be
(1/10) x (639 + 50) = (1/10) x (689) = <u>68.9%</u> .
In general, your overall score for the class, after the final, is going to be
63.9% plus (1 tenth) of your score on the final.
Good luck !
