What is greater 9,000 g or 8 kg

Randomly selected 110 student cars have ages with a mean of 8 years and a standard deviation of 3.6 years, while randomly select

monitta

Answer:

1. Yes, there is sufficient evidence to support the claim that student cars are older than faculty cars.

2. The 98% confidence interval for the difference between the two population means is [1.432 years, 3.968 years].

Step-by-step explanation:

We are given that randomly selected 110 student cars to have ages with a mean of 8 years and a standard deviation of 3.6 years, while randomly selected 75 faculty cars to have ages with a mean of 5.3 years and a standard deviation of 3.7 years.

Let $\mu_1$ = mean age of student cars.

$\mu_2$ = mean age of faculty cars.

So, Null Hypothesis, 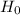$H_0$ : $\mu_1 \leq \mu_2$ {means that the student cars are younger than or equal to faculty cars}

Alternate Hypothesis, $H_A$ : $\mu_1>\mu_2$ {means that the student cars are older than faculty cars}

(1) The test statistics that will be used here is Two-sample t-test statistics because we don't know about the population standard deviations;

T.S. = $\frac{(\bar X_1-\bar X_2)-(\mu_1-\mu_2)} {s_p \times \sqrt{\frac{1}{n_1}+\frac{1}{n_2} } }$ ~ $t_n_1_+_n_2_-_2$

where, $\bar X_1$ = sample mean age of student cars = 8 years

$\bar X_2$ = sample mean age of faculty cars = 5.3 years

$s_1$ = sample standard deviation of student cars = 3.6 years

$s_2$ = sample standard deviation of student cars = 3.7 years

$n_1$ = sample of student cars = 110

$n_2$ = sample of faculty cars = 75

Also, $s_p=\sqrt{\frac{(n_1-1)\times s_1^{2}+(n_2-1)\times s_2^{2} }{n_1+n_2-2} }$ = $\sqrt{\frac{(110-1)\times 3.6^{2}+(75-1)\times 3.7^{2} }{110+75-2} }$ = 3.641

So, the test statistics = $\frac{(8-5.3)-(0)} {3.641 \times \sqrt{\frac{1}{110}+\frac{1}{75} } }$ ~ $t_1_8_3$

= 4.952

The value of t-test statistics is 4.952.

Since the value of our test statistics is more than the critical value of t, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region.

Therefore, we support the claim that student cars are older than faculty cars.

(2) The 98% confidence interval for the difference between the two population means ( $\mu_1-\mu_2$ ) is given by;

98% C.I. for ( $\mu_1-\mu_2$ ) = $(\bar X_1-\bar X_2) \pm (t_(_\frac{\alpha}{2}_) \times s_p \times \sqrt{\frac{1}{n_1}+\frac{1}{n_2} })$

= $(8-5.3) \pm (2.326 \times 3.641 \times \sqrt{\frac{1}{110}+\frac{1}{75} })$

= $[2.7 \pm 1.268]$

= [1.432, 3.968]

Here, the critical value of t at a 1% level of significance is 2.326.

Hence, the 98% confidence interval for the difference between the two population means is [1.432 years, 3.968 years].

7 0

3 years ago

If 2> -a, then a < -2. True False

Nonamiya [84]

Answer:

False

Step-by-step explanation:

Flip the equation.

−a<2

Divide both sides by -1.

a>−2

4 0

3 years ago

D

Anestetic [448]

Answer:

D. 1

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

Brackets
Parenthesis
Exponents
Multiplication
Division
Addition
Subtraction

Left to Right

Algebra I

Function Notation

Pre-Calculus

Unit Circle

Calculus

Derivatives
Derivative Notation
Derivative of tan(x) = sec²(x)

Step-by-step explanation:

Step 1: Define

$\frac{d}{dx} [tan(x)]\\x = \pi$

Step 2: Differentiate

Differentiate: $\frac{d}{dx} [tan(x)] = sec^2(x)$

Step 3: Evaluate

Substitute in x: $sec^2(\pi)$
Evaluate: $1$

7 0

3 years ago

Can someone help me out my grads are bad

Talja [164]

Answer:

8cm

Step-by-step explanation:

length × height

4×2 = 8cm

6 0

3 years ago

Read 2 more answers

Which two values of x are the roots of the polynomial below? x^2+5x+11

In-s [12.5K]

Answer:

x = -5/2 + i√19 and x = -5/2 - i√19

Step-by-step explanation:

Next time, please share the possible answer choices.

Here we can actually find the roots, using the quadratic formula or some other approach.

a = 1, b = 5 and c = 11. Then the discriminant is b^2-4ac, or 5^2-4(1)(11). Since the discriminant is negative, the roots are complex. The discriminant value is 25-44, or -19.

Thus, the roots of the given poly are:

-5 plus or minus i√19

x = -----------------------------------

2(1)

or x = -5/2 + i√19 and x = -5/2 - i√19

5 0

3 years ago

Read 2 more answers