De

Find the area of the following<br> kite:<br> A = [?] m²<br> 40 m<br> 16 m<br> 16 m<br> 6 m

Rama09 [41]

Answer:

$Area_{kite}=736m^2$

Step-by-step explanation:

There are a few methods to find the area of this figure:

1. kite area formula

2. 2 triangles (one top, one bottom)

3. 2 triangles (one left, one right)

4. 4 separate right triangles.

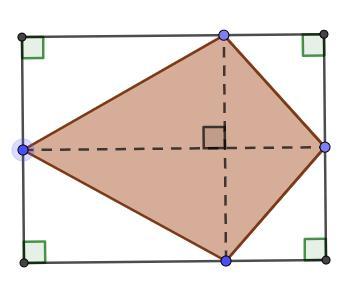
<h3><u>Option 1: The kite area formula</u></h3>

Recall the formula for area of a kite: $Area_{kite}=\frac{1}{2} d_{1}d_{2}$ where d1 and d2 are the lengths of the diagonals of the kite ("diagonals" are segments that connect non-adjacent vertices -- in a quadrilateral, vertices that are across from each other).

If you've forgotten why that is the formula for the area of a kite, observe the attached diagram: note that the kite (shaded in) is half of the area of the rectangle that surrounds the kite (visualize the 4 smaller rectangles, and observe that the shaded portion is half of each, and thus the area of the kite is half the area of the large rectangle).

The area of a rectangle is $Area_{rectangle}=bh$ , sometimes written as $Area_{rectangle}=bh$ , where w is the width, and h is the height of the rectangle.

In the diagram, notice that the width and height are each just the diagonals of the kite. So, the <u>Area of the kite</u> is <u>half of the area of that surrounding rectangle</u> ... the rectangle with sides the lengths of the kite's diagonals.Hence, $Area_{kite}=\frac{1}{2} d_{1}d_{2}$

For our situation, each of the diagonals is already broken up into two parts from the intersection of the diagonals. To find the full length of the diagonal, add each part together:

For the horizontal diagonal (which I'll call d1): $d_{1}=40m+6m=46m$

For the vertical diagonal (which I'll call d2): $d_{2}=16m+16m=32m$

Substituting back into the formula for the area of a kite:

$Area_{kite}=\frac{1}{2} d_{1}d_{2}\\Area_{kite}=\frac{1}{2} (46m)(32m)\\Area_{kite}=736m^2$

<h3><u /></h3><h3><u>Option 2: The sum of the parts (version 1)</u></h3>

If one doesn't remember the formula for the area of a kite, and can't remember how to build it, the given shape could be visualized as 2 separate triangles, the given shape could be visualized as 2 separate triangles (one on top; one on bottom).

Visualizing it in this way produces two congruent triangles. Since the upper and lower triangles are congruent, they have the same area, and thus the area of the kite is double the area of the upper triangle.

Recall the formula for area of a triangle: $Area_{triangle}=\frac{1}{2} bh$ where b is the base of a triangle, and h is the height of the triangle <em>(length of a perpendicular line segment between a point on the line containing the base, and the non-colinear vertex)</em>. Since all kites have diagonals that are perpendicular to each other (as already indicated in the diagram), the height is already given (16m).

The base of the upper triangle, is the sum of the two segments that compose it: $b=40m+6m=46m$

<u>Finding the Area of the upper triangle</u> $Area_{\text{upper }triangle}=\frac{1}{2} (46m)(16m) = 368m^2$

<u>Finding the Area of the kite</u>

$Area_{kite}=2*(368m^2)$

$Area_{kite}=736m^2$

<h3><u>Option 3: The sum of the parts (version 2)</u></h3>

The given shape could be visualized as 2 separate triangles (one on the left; one on the right). Each triangle has its own area, and the sum of both triangle areas is the area of the kite.

<em>Note: In this visualization, the two triangles are not congruent, so it is not possible to double one of their areas to find the area of the kite.</em>

The base of the left triangle is the vertical line segment the is the vertical diagonal of the kite. We'll need to add together the two segments that compose it: $b=16m+16m=32m$ . This is also the base of the triangle on the right.

<u>Finding the Area of left and right triangles</u>

$Area_{\text{left }triangle}=\frac{1}{2} (32m)(40m) = 640m^2$

The base of the right triangle is the same length as the left triangle: $Area_{\text{right }triangle}=\frac{1}{2} (32m)(6m) = 96m^2$

<u>Finding the Area of the kite</u>

$Area_{kite}=(640m^2)+(96m^2)$

$Area_{kite}=736m^2$

<h3><u>Option 4: The sum of the parts (version 3)</u></h3>

If you don't happen to see those composite triangles from option 2 or 3 when you're working this out on a particular problem, the given shape could be visualized as 4 separate right triangles, and we're still given enough information in this problem to solve it this way.

<u>Calculating the area of the 4 right triangles</u>

$Area_{\text{upper left }triangle}=\frac{1}{2} (40m)(16m) = 320m^2$

$Area_{\text{upper right }triangle}=\frac{1}{2} (6m)(16m) = 48m^2$

$Area_{\text{lower left }triangle}=\frac{1}{2} (40m)(16m) = 320m^2$

$Area_{\text{lower right }triangle}=\frac{1}{2} (6m)(16m) = 48m^2$

<u>Calculating the area of the kite</u>

$Area_{kite}=(320m^2)+(48m^2)+(320m^2)+(48m^2)$

$Area_{kite}=736m^2$

8 0

2 years ago

Need help please <br><br>how do you know what the coordinates are of the vertex?

kvv77 [185]

Answer:

The vertex is the point (0,0)

Step-by-step explanation:

The zero, or place that the graph passes/sits on the X-Axis is at the point (0,0)

4 0

3 years ago

Read 2 more answers

Valuate 3a2 + 4b2 for a = 2 and b = 3

k0ka [10]

Answer:

48

Step-by-step explanation:

3(22)+4(32)

=(3)(4)+4(32)

=12+4(32)

=12+(4)(9)

=12+36

=48

4 0

3 years ago

Find the equation of the line that passes through the point left-parenthesis 1 comma 8 right-parenthesis and is perpendicular to

Furkat [3]

Don't be shy about using actual parentheses and commas.

Line through (1,8) perpendicular to

$-\dfrac 4 5 x + \dfrac 5 4 y = -4$

The perpendicular family is gotten by swapping the coefficients on x and y, negating exactly one of them. The constant is given directly by the point we're through:

$\dfrac 5 4 x + \dfrac 4 5 y = \dfrac 5 4 (1) + \dfrac 4 5 (8) = \dfrac 5 4 + \dfrac{32}{5}$

Let's clear the fractions by multiplying both sides by 20.

$25x + 16y = 25 + 128 = 153$

Might as well stop here.

Answer: 25 x + 16 y = 153

7 0

3 years ago

The functions f and g are defined as follows.

mariarad [96]

Answer:

x != -2, x^2 + 1, 1/5

Step-by-step explanation:

(a) It can be understood that nothing can divide 0

thus denominator cannot be 0 meaning x cannot be -2.

(-2 + 2) = 0

(b) y = sqrt(x-1)

inverse meaning we make x the subject

square both sides

y^2 = x - 1

y^2 + 1 = x

inverse = x^2 + 1

(c) composite function:

pass g(10) as domain of f

g(10) = 3, f(3) = 1/(5) = 1/5

6 0

3 years ago