Complete Question:
An instant lottery game card consists of six disks labeled A, B, C, D, E,F. The game is played by purchasing a game card and scratching off two disks. Each of five of the disks hides $., and one of the disks hides $.. The total of the amounts on the two disks that are scratched off is paid to the person who purchased the card.
1. What are the possible total amounts of money you could win if you scratch off two disks?
2. If you pick two disks at random:
a. How likely is it that you win $2.00?
b. How likely is it that you win $11.00?
3. Based on Exercise 2, how much should you expect to win on average per game if you played this game a large
number of times?
4. To play the game, you must purchase a game card. The price of the card is set so that the game is fair. What do you
think is meant by a fair game in the context of playing this instant lottery game?
5. How much should you be willing to pay for a game card if the game is to be a fair one? Explain.
Answer:
1. $2 or $11
2a.
2b. kjhdj
3 $5
Step-by-step explanation:
First Question :
What are the possible total amounts of money you could win if you scratch off two disks?
Explained solution :
If you uncovered two $. disks, the total is $.
If uncovered one $. disk and you also uncovered the $. disk, the total is $..
Second Question:
2. If you pick two disks at random:
a. How likely is it that you win $2.00?
b. How likely is it that you win $11.00?
Explained Answer:
If you pick two disks at random:
a. How likely is it that you win $.?
b. How likely is it that you win $.?
These is one of the many ways to determine the probabilities of getting $. and $..
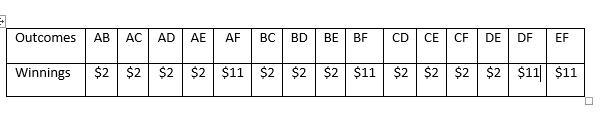
List the possible pairs of scratched disks in a sample space, , keeping in mind that two different disks need to be scratched, and the order of choosing them does not matter. For example, you could use the notation that indicates disk and disk were chosen, in either order. = {,,,,,,,,,,,,,,}
There are different ways of choosing two disks without replacement and without regard to order from the six possible disks.
Identify the winning amount for each choice under the outcome in . Suppose that disks – hide $., and disk hides $..
The possible ways of selection and the winning amounts for each is shown on the table below(i.e. the uploaded image)
Since each of the outcomes in is equally likely, the probability of winning $. is the number of ways of winning $., namely, , out of the total number of possible outcomes, .
Similarly,
In the case where its difficult to list out the possible way of selecting each disk we can apply this method :
Recall that counting when sampling was done without replacement and without regard to order involved combinations.
The number of ways of choosing two disks without replacement and without regard to order is <em /><em>C</em>= (n<em></em> denotes the number of combinations of items taken at a time without replacement and without regard to order. i.e the number of way of selecting from n items taken these items k at a time without replacement )
To win $., two disks need to be chosen from the five $. disks. The number of ways of doing that is <em />=
So, the probability of winning $. is
To win $., one disk needs to be chosen from the five $. disks, and the $. disk needs to be chosen. The number of ways of doing that is (<em />)(<em />)
(<em />) = 5
(<em />) = 1
(<em />)(<em />) = 5×1 = 5
So, the probability of winning $. is
No 3
Based on Exercise 2, how much should you expect to win on average per game if you played this game a large number of times?
The expected winning amount per play is $..
No 4
To play the game, you must purchase a game card. The price of the card is set so that the game is fair. What do you think is meant by a fair game in the context of playing this instant lottery game?
A fair game in this context means that the cost to play the game should be equal to the expected winnings
No 5
How much should you be willing to pay for a game card if the game is to be a fair one? Explain.
In the context of this instant lottery game, the game is fair if the player is willing to pay $. (the expected winning per play) to purchase each game card.