2100|2
1050|2
525|3
175|5
35|5
7|7
1|
2100 = 2 × 2 × 3 × 5 × 5 × 7 = 2² × 3 × 5² × 7
First exercise:
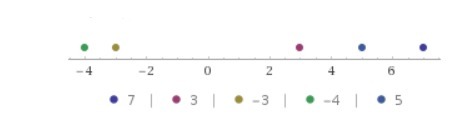
a. The first prime numbers are 2,3,5,7,11,... So, the greatest prime interger between 4 and 9 is 7. A = 7.
b. Since the number line's growing direction is rightwards, going to the left means to decrease. So, point E is 4 less than point A, i.e. 7-4 = 3. E = 3.
c. The additive inverse of a number  is another number
is another number  such that
such that  . So, we're looking form a number such that
. So, we're looking form a number such that  , and thus O = - 3.
, and thus O = - 3.
d. This point looks a bit ambiguous to me honestly. We know that IO = 2, which I presume means that the points I and O are two units apart, but we're not told if I is two units left or right with respect to O. To solve this issue, I'm assuming that IO implies that I sits before O, and so I is two units left with respect to O. As we said in point a., two units left means two less, so we have I = -3-2 = -5. At this point, point L is halfway between -5 and -3, and thus L = - 4.
e. The sum of the coordinates of A and E is 7 + 3 = 10. Half that sum is 5, so M = 5.
In the attached image, you can see the number line filled with the points asked by the exercise.
Second exercise:
All the requests can be written as an equation in which we look for the values of x. Below you find the equation and the solutions.





A little side note: I've honestly never met the expression "subtract A to B", but always "subtract A from B". I assumed they mean the same thing, but if anybody thinks I'm wrong please let me know! (I'm not a native speaker, so I can only refer to the math I met during my studies).
The answer is C
First you subtract 44,604 from 1,715,760 to get 1,671,156 then you divide 1,671,156 by 27,396 to get 61 people