Answer:
Step-by-step explanation:
first method is to try out all possible combinations and pick out the best one which has the minimum operations but that would be infeasible method if the no of matrices increases
so the best method would be using the dynamic programming approach.
A1 = 100 x 50
A2 = 50 x 200
A3 = 200 x 50
A4 = 50 x 10
Table M can be filled using the following formula
Ai(m,n)
Aj(n,k)
M[i,j]=m*n*k
The matrix should be filled diagonally i.e., filled in this order
(1,1),(2,2)(3,3)(4,4)
(2,1)(3,2)(4,3)
(3,1)(4,2)
(4,1)
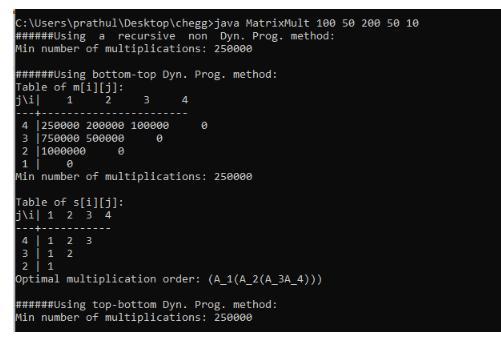
<u> Table M[i, j] </u>
1 2 3 4
4 250000 200000 100000 0
3
750000 500000 0
2 1000000 0
1
0
Table S can filled this way
Min(m[(Ai*Aj),(Ak)],m[(Ai)(Aj*Ak)])
The matrix which is divided to get the minimum calculation is selected.
Table S[i, j]
1 2 3
4
4 1 2 3
3
1 2
2 1
1
After getting the S table the element which is present in (4,1) is key for dividing.
So the matrix multiplication chain will be (A1 (A2 * A3 * A4))
Now the element in (4,2) is 2 so it is the key for dividing the chain
So the matrix multiplication chain will be (A1 (A2 ( A3 * A4 )))
Min number of multiplications: 250000
Optimal multiplication order: (A1 (A2 ( A3 * A4 )))
to get these calculations perform automatically we can use java
code:
public class MatrixMult
{
public static int[][] m;
public static int[][] s;
public static void main(String[] args)
{
int[] p = getMatrixSizes(args);
int n = p.length-1;
if (n < 2 || n > 15)
{
System.out.println("Wrong input");
System.exit(0);
}
System.out.println("######Using a recursive non Dyn. Prog. method:");
int mm = RMC(p, 1, n);
System.out.println("Min number of multiplications: " + mm + "\n");
System.out.println("######Using bottom-top Dyn. Prog. method:");
MCO(p);
System.out.println("Table of m[i][j]:");
System.out.print("j\\i|");
for (int i=1; i<=n; i++)
System.out.printf("%5d ", i);
System.out.print("\n---+");
for (int i=1; i<=6*n-1; i++)
System.out.print("-");
System.out.println();
for (int j=n; j>=1; j--)
{
System.out.print(" " + j + " |");
for (int i=1; i<=j; i++)
System.out.printf("%5d ", m[i][j]);
System.out.println();
}
System.out.println("Min number of multiplications: " + m[1][n] + "\n");
System.out.println("Table of s[i][j]:");
System.out.print("j\\i|");
for (int i=1; i<=n; i++)
System.out.printf("%2d ", i);
System.out.print("\n---+");
for (int i=1; i<=3*n-1; i++)
System.out.print("-");
System.out.println();
for (int j=n; j>=2; j--)
{
System.out.print(" " + j + " |");
for (int i=1; i<=j-1; i++)
System.out.printf("%2d ", s[i][j]);
System.out.println();
}
System.out.print("Optimal multiplication order: ");
MCM(s, 1, n);
System.out.println("\n");
System.out.println("######Using top-bottom Dyn. Prog. method:");
mm = MMC(p);
System.out.println("Min number of multiplications: " + mm);
}
public static int RMC(int[] p, int i, int j)
{
if (i == j) return(0);
int m_ij = Integer.MAX_VALUE;
for (int k=i; k<j; k++)
{
int q = RMC(p, i, k) + RMC(p, k+1, j) + p[i-1]*p[k]*p[j];
if (q < m_ij)
m_ij = q;
}
return(m_ij);
}
public static void MCO(int[] p)
{
int n = p.length-1; // # of matrices in the product
m = new int[n+1][n+1]; // create and automatically initialize array m
s = new int[n+1][n+1];
for (int l=2; l<=n; l++)
{
for (int i=1; i<=n-l+1; i++)
{
int j=i+l-1;
m[i][j] = Integer.MAX_VALUE;
for (int k=i; k<=j-1; k++)
{
int q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
if (q < m[i][j])
{
m[i][j] = q;
s[i][j] = k;
}
}
}
}
}
public static void MCM(int[][] s, int i, int j)
{
if (i == j) System.out.print("A_" + i);
else
{
System.out.print("(");
MCM(s, i, s[i][j]);
MCM(s, s[i][j]+1, j);
System.out.print(")");
}
}
public static int MMC(int[] p)
{
int n = p.length-1;
m = new int[n+1][n+1];
for (int i=0; i<=n; i++)
for (int j=i; j<=n; j++)
m[i][j] = Integer.MAX_VALUE;
return(LC(p, 1, n));
}
public static int LC(int[] p, int i, int j)
{
if (m[i][j] < Integer.MAX_VALUE) return(m[i][j]);
if (i == j) m[i][j] = 0;
else
{
for (int k=i; k<j; k++)
{
int q = LC(p, i, k) + LC(p, k+1, j) + p[i-1]*p[k]*p[j];
if (q < m[i][j])
m[i][j] = q;
}
}
return(m[i][j]);
}
public static int[] getMatrixSizes(String[] ss)
{
int k = ss.length;
if (k == 0)
{
System.out.println("No matrix dimensions entered");
System.exit(0);
}
int[] p = new int[k];
for (int i=0; i<k; i++)
{
try
{
p[i] = Integer.parseInt(ss[i]);
if (p[i] <= 0)
{
System.out.println("Illegal input number " + k);
System.exit(0);
}
}
catch(NumberFormatException e)
{
System.out.println("Illegal input token " + ss[i]);
System.exit(0);
}
}
return(p);
}
}
output: