Answer: The correct answer is: [B]:
____________________________________________
→ " 35 square units " .
____________________________________________
{or; write as: " 35 sq units " ; or; " 35 units² " .}.
____________________________________________
Step-by-step explanation:
____________________________________________
Note that the area, "A" ; of a "parallelogram" ;
→ {for which we wish to solve} ;
→ can be calculated by using the formula:
____________________________________________
→ " A = b * h " ;
→ { that is: " Area = base * height " } ;
→ in which:
____________________________________________
→ "A" is the "area" [of the parallelogram] ;
in: [ "square units" ; or: "sq units" ; or: "units² " ] ;
____________________________________________
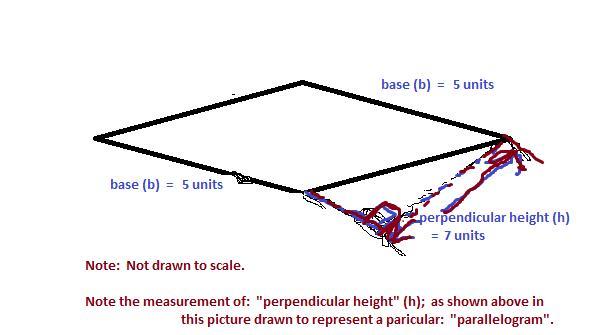
→ "b" is the "base length" (of one of the bases of the parallelogram) ;
{Note that both bases of a parallelogram have equal lengths.
— Refer to "image attached" for additional information.}.
____________________________________________
→ "h" is the "perpendicular height" [of the parallelogram] ;
____________________________________________
<u>Note</u>:
- All rectangles are parallelograms, but not all parallelograms are rectangles.
- All squares are rectangles, but not all rectangles are squares.
____________________________________________
So, let us consider a "rectangle" that is not a square;
→ but has 4 (four) right angles; as follows:
____________________________________________
Rough sketch:
base (b)
---------------------------
| | height (h)
|_____________ |
____________________________________________
The formula (equation) for the area, "A" ; of a rectangle is:
→ " A = b * h " ;
→ { that is: " Area = base * height " .} .
→ Since a rectangle is a parallelogram;
→ The formula (equation) for the area, "A" ;
for <u><em>Any parallelogram</em></u> <u><em>is the same</em></u> :
→ " A = b * h " ;
→ { that is: " Area = base * height " .} .
____________________________________________
→ However, it is important to remember that the formula/equation for the "area, "A" ; for <em><u>any parallelogram</u></em> — [<em><u>including All rectangles</u></em>] — is actually:
→ " A = b * h " ; that is: " <u>Area = base * [perpendicular] height</u> " .
____________________________________________
Note that we are Not Given Any "image attached" that represents the: "parallelogram" —
<u>Note</u>: Refer to the text within "this very Brainly question being asked" ; that is; the following text:
____________________________________________
"the parallelogram ABCD" that is "shown below" {sic} ; as stated within the question.
____________________________________________
Nonetheless:
We are given:
h (height) = 7 units ; And:
b (base) = 5 units. ;
<em><u>For our purposes</u></em>, let us assume that the given "height, "h" = 7 units" ;
→ refers to the "<u><em>perpendicular height </em></u>" ;
Now, we can calculate the "Area; A" ; in "square units" ; as follows:
___________________________________________
→ " A = b * h " ; Solve for: "A" ;
Plug in our given values for "b" and "h" ; to solve for "A" ;
→ " A = (5 units) * (7 units) " ;
= 5 * 7 * units * units " ;
" A = 35 units² ;
or: " 35 square units " ;
→ which is:
___________________________________________
Answer choice: [B]: " 35 square units " .
___________________________________________
<u>Note</u>: Refer to "image attached" ; to refer to: "<em><u>perpendicular height</u></em><em> </em>" — as regards to many "traditional" types of " <em><u>parallelograms</u></em> " .
___________________________________________
Hope this helps!
Best wishes to you in your academic pursuits
— and within the "Brainly" community, as well!
___________________________________________