Answer:
Yes, there is a difference between the population mean for the math scores and the population mean for the writing scores.
Test Statistics =  follows
follows  .
.
Step-by-step explanation:
We are provided with the sample data showing the math and writing scores for a sample of twelve students who took the SAT ;
Let A = Math Scores ,B = Writing Scores and D = difference between both
So,  = Population mean for the math scores
= Population mean for the math scores
 = Population mean for the writing scores
= Population mean for the writing scores
Let  = Difference between the population mean for the math scores and the population mean for the writing scores.
= Difference between the population mean for the math scores and the population mean for the writing scores.
<em> Null Hypothesis, </em>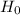 <em> : </em>
<em> : </em> <em> or </em>
<em> or </em> <em> = 0 </em>
<em> = 0 </em>
<em> Alternate Hypothesis, </em>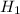 <em> : </em>
<em> : </em> <em> or </em>
<em> or </em> <em> 0</em>
<em> 0</em>
Hence, Test Statistics used here will be;
 follows
follows  where, Dbar = Bbar - Abar
where, Dbar = Bbar - Abar
 =
= 
n = 12
Student Math scores (A) Writing scores (B) D = B - A
1 540 474 -66
2 432 380 -52
3 528 463 -65
4 574 612 38
5 448 420 -28
6 502 526 24
7 480 430 -50
8 499 459 -40
9 610 615 5
10 572 541 -31
11 390 335 -55
12 593 613 20
Now Dbar = Bbar - Abar = 489 - 514 = -25
Bbar =  =
=  = 489
= 489
Abar =  =
=  = 514
= 514
∑ = 22600 and
= 22600 and  =
=  =
=  = 37.05
= 37.05
So, Test statistics =  follows
follows 
=  follows
follows  = -2.34
= -2.34
<em>Now at 5% level of significance our t table is giving critical values of -2.201 and 2.201 for two tail test. Since our test statistics doesn't fall between these two values as it is less than -2.201 so we have sufficient evidence to reject null hypothesis as our test statistics fall in the rejection region .</em>
Therefore, we conclude that there is a difference between the population mean for the math scores and the population mean for the writing scores.