a) The electric force exerted by S1 on S2 is 21.58μN.
In this case we are talking about two different types of charges, a positive charge and a negative charge, therefore, they are sensing a force of attraction.
The magnitude of the force is determined by using the following formula:
where:
= Electric force [N]
= Electric constant ()
= First charge [C]
= Second charge [C]
r = distance between the two charges
So, in this case, the force can be calculated like this:
So the force will be equal to:
which is the same as:
b) The electric field created by S1 at the level of S2 is
The electric field tells us how many Newtons of force can be applied on a given point in space per unit of charge caused by an existing electric charge. From the concept, we can take the following formula for the electric field.
where:
= electric field generated by the first sphere.
which yields:
When talking about electric fields, we know what their direction is if we suppose the electric field is always affecting a positive charge in the given point in space. In this case, since S1 is positive, we can asume the electric field is in a direction away from S1.
c)
The electric potential created by S1 at the level or S2 is 360V
Electric potential is defined to be the amount of energy you will have at a given point per electric charge. This electric potential can be found by using the following formula:
V=Er
Where V is the electric potential and it is given in volts.
- Volts are defined to be 1 Joule per Coulomb. Energy by electric charge.
So we can use the data found in the previous sections to find the electric potential:
V=360V
d) The force exerted by S2 on S1 will be the same in magnitude as the force exerted by S1 on S2 but oposite in direction. This is because the force will depend on the two charges, and the distance between them, so:
The electric force exerted by S1 on S2 is 21.58μN.
The magnitude of the force is determined by using the following formula:
So the force will be equal to:
which is the same as:
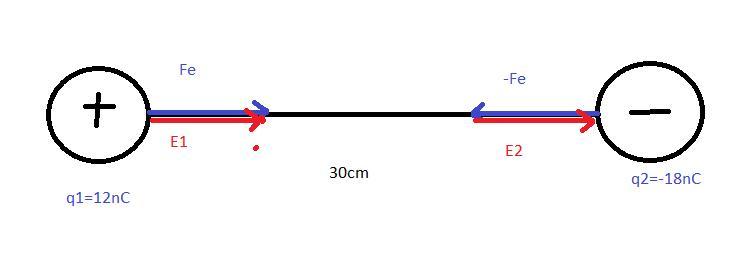
e) The electric field generated by S1 in the middle of S1 and S2 is
In order to find the electric field generated by S1, we can make use of the following formula
which yields:
f) The electric field in the middle of S1 and S2 is
In order to find the electric field generated by two different charges at a given point is found by using the following formula:
where:
= each of the charges in the system
= the distance between each of the charges and the point we are analyzing.
Since the electric field is a vector, we need to take into account the individual electric fields' directions. In this case we suppose we have a positive test charge between the two charges. We can see that the positive test charge will sense a force in the same direction independently on if the force is excerted by the positive charge or the negative charge. Therefore both electric fields will have the same direction. We'll suppose the electric fields will be positive then, so:
which yields:
g) The electric potential in the middle of S1 and S2 is 1.80 kV
Since we know what the electric field is from the previous question, we can make use of the same formula we used before to find the electric potential in the middle of S1 and S2
So let's take the formula:
V=Er
So we can use the data found in the previous sections to find the electric potential:
V=1.80kV
h)
The electric potential generated by S2 on the position of S1 is 539.4V and can be found by using the following formula:
So we can use the data provided by the problem to find the electric potential.
V=539.4V