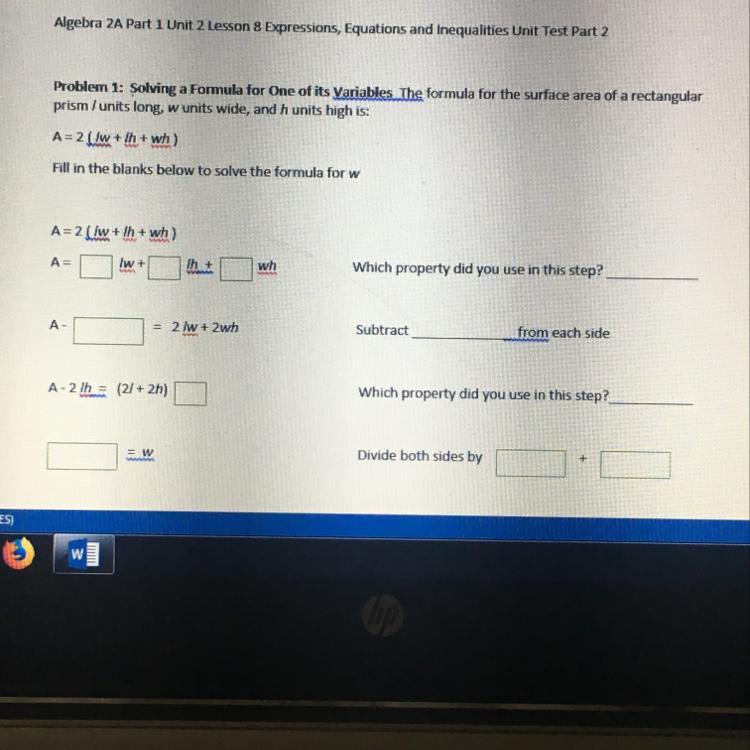
Answer:
- Function 1 is not a function.
- The domain and range of the first function respectively are
and
.
- Function 2 is a function.
- The domain and range of the second function respectively are
and
.
Step-by-step explanation:
In math, every function has a domain and a range.
- The domain of the function is all of the x-values for which the function is true. These can be found on the x-axis for every position at which the function exists or crosses the x-axis.
- The range of the function is all of the y-values for which the function is defined. The range can be found in the same manner as the domain - for every y-value at which the function exists, it is apart of the range.
Therefore, with this information given to us, we need to also know about coordinate pairs. Coordinate pairs are written in (x, y) form.
Functions are classified in four ways:
- One-to-one functions: Functions are considered to be one-to-one functions if there are unique y-values (no y-values are repeated) and there is one x-value for every one y-value.
- Onto functions: Functions are considered to be onto functions if there are unique x-values. These x-values cannot repeat, but different x-values can be connected to the same y-values.
- Both one-to-one & onto: Functions are considered both one-to-one and onto when there is exactly one x-value for every one y-value.
- Neither one-to-one or onto: Functions are considered to be neither an one-to-one function or an onto function when they have two or more of the same y-values assigned to the same x-values. A function cannot exist if y-values are duplicated on a x-value.
Finally, the domain and range should be written in ascending order. Therefore, the lowest number should be written first in the domain and the highest number should be written last.
<u>Function 1</u>
We are given the function: .
Using the information above, we can pick out our x and y-values from the function.
Values of Domain: -3, 1, 0, 1, 5
Values of Range: 3, 1, -2, -4, -1
Now, we need to arrange these in ascending order.
Domain Rearranged: -3, 0, 1, 1, 5
Range Rearranged: -4, -2, -1, 1, 3
Using these values, we can see what values we have.
For x-values:
x = -3: 1 value
x = 0: 1 value
x = 1: 2 values
x = 5: 1 value
For y-values:
y = -4: 1 value
y = -2: 1 value
y = -1: 1 value
y = 1: 1 value
y = 3: 1 value
Therefore, we can begin classifying this function. Because we have all separate y-values, we have a function. However, we have two of the same x-value, so we have an onto function.
Now, we can create our domain and range in the set. We use the same formatting given for the first function. We list the values in ascending order and list them in brackets to show that they are apart of a set.
The domain values are the x-values, so they are .
The range values are the y-values, so they are .
Therefore, the domain and range for function one are defined, but this is not a function. Because the x-values repeat, it cannot be a function.
<u>Function 2</u>
We are given a table of values that needs to be translated into the set notation. This makes it easier to identify the values. We are given x-coordinates in the top row and y-coordinates in the bottom row. And, the table is set up to where the x-value directly above the y-value makes a coordinate pair. Using this, we can create the set function.
The set function is .
Now, we can use the same method as above to pick out the x and y-values and reorder them to be from least to greatest.
Values of Domain: -2, -1, 0, 1, 2
Values of Range: -7, -2, 1, -2, -7
Now, we rearrange these.
Domain Rearranged: -2, -1, 0, 1, 2
Range Rearranged: -7, -7, -2, -2, 1
Now, we can check how many times the function presents each coordinate.
For x-values:
x = -2: 1 value
x = -1: 1 value
x = 0: 1 value
x = 1: 1 value
x = 2: 1 value
For y-values:
y = -7: 2 values
y = -2: 2 values
y = 1: 1 value
Now, we can classify the function. The x-values are unique, but the y-values are repeated. Therefore, because the x-values are assigned to one y-coordinate and they are unique, this is not an one-to-one function. Additionally, it cannot be an onto function because the y-values are not unique - they are repeated. Therefore, it is neither an one-to-one function or an onto function. If this function were graphed, it would actually reveal a parabola. However, it is still a function.
The domain values are the x-values, so they are .
The range values are the x-values, so they are .