2865 students participated in a competitive exam. There were 60 rooms in the

The graph of f(x)= 3/1+x^2 is shown in the figure to the right. Use the second derivative of f to find the intervals on which f

GenaCL600 [577]

Answer:

Concave Up Interval: $(- \infty,\frac{-\sqrt{3} }{3} )U(\frac{\sqrt{3} }{3} , \infty)$

Concave Down Interval: $(\frac{-\sqrt{3} }{3}, \frac{\sqrt{3} }{3} )$

General Formulas and Concepts:

Calculus

Derivative of a Constant is 0.

Basic Power Rule:

f(x) = cxⁿ
f’(x) = c·nxⁿ⁻¹

Quotient Rule: $\frac{d}{dx} [\frac{f(x)}{g(x)} ]=\frac{g(x)f'(x)-g'(x)f(x)}{g^2(x)}$

Chain Rule: $\frac{d}{dx}[f(g(x))] =f'(g(x)) \cdot g'(x)$

Second Derivative Test:

Possible Points of Inflection (P.P.I) - Tells us the possible x-values where the graph f(x) may change concavity. Occurs when f"(x) = 0 or undefined
Points of Inflection (P.I) - Actual x-values when the graph f(x) changes concavity
Number Line Test - Helps us determine whether a P.P.I is a P.I

Step-by-step explanation:

Step 1: Define

$f(x)=\frac{3}{1+x^2}$

Step 2: Find 2nd Derivative

1st Derivative [Quotient/Chain/Basic]: $f'(x)=\frac{0(1+x^2)-2x \cdot 3}{(1+x^2)^2}$
Simplify 1st Derivative: $f'(x)=\frac{-6x}{(1+x^2)^2}$
2nd Derivative [Quotient/Chain/Basic]: $f"(x)=\frac{-6(1+x^2)^2-2(1+x^2) \cdot 2x \cdot -6x}{((1+x^2)^2)^2}$
Simplify 2nd Derivative: $f"(x)=\frac{6(3x^2-1)}{(1+x^2)^3}$

Step 3: Find P.P.I

Set f"(x) equal to zero: $0=\frac{6(3x^2-1)}{(1+x^2)^3}$

Case 1: f" is 0

Solve Numerator: $0=6(3x^2-1)$
Divide 6: $0=3x^2-1$
Add 1: $1=3x^2$
Divide 3: $\frac{1}{3} =x^2$
Square root: $\pm \sqrt{\frac{1}{3}} =x$
Simplify: $\pm \frac{\sqrt{3}}{3} =x$
Rewrite: $x= \pm \frac{\sqrt{3}}{3}$

Case 2: f" is undefined

Solve Denominator: $0=(1+x^2)^3$
Cube root: $0=1+x^2$
Subtract 1: $-1=x^2$

We don't go into imaginary numbers when dealing with the 2nd Derivative Test, so our P.P.I is $x= \pm \frac{\sqrt{3}}{3}$ (x ≈ ±0.57735).

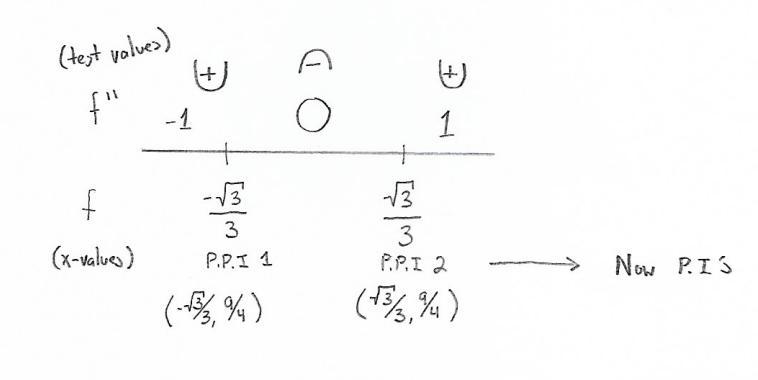
Step 4: Number Line Test

See Attachment.

We plug in the test points into the 2nd Derivative and see if the P.P.I is a P.I.

x = -1

Substitute: $f"(x)=\frac{6(3(-1)^2-1)}{(1+(-1)^2)^3}$
Exponents: $f"(x)=\frac{6(3(1)-1)}{(1+1)^3}$
Multiply: $f"(x)=\frac{6(3-1)}{(1+1)^3}$
Subtract/Add: $f"(x)=\frac{6(2)}{(2)^3}$
Exponents: $f"(x)=\frac{6(2)}{8}$
Multiply: $f"(x)=\frac{12}{8}$
Simplify: $f"(x)=\frac{3}{2}$

This means that the graph f(x) is concave up before $x=\frac{-\sqrt{3}}{3}$ .

x = 0

Substitute: $f"(x)=\frac{6(3(0)^2-1)}{(1+(0)^2)^3}$
Exponents: $f"(x)=\frac{6(3(0)-1)}{(1+0)^3}$
Multiply: $f"(x)=\frac{6(0-1)}{(1+0)^3}$
Subtract/Add: $f"(x)=\frac{6(-1)}{(1)^3}$
Exponents: $f"(x)=\frac{6(-1)}{1}$
Multiply: $f"(x)=\frac{-6}{1}$
Divide: $f"(x)=-6$

This means that the graph f(x) is concave down between and .

x = 1

Substitute: $f"(x)=\frac{6(3(1)^2-1)}{(1+(1)^2)^3}$
Exponents: $f"(x)=\frac{6(3(1)-1)}{(1+1)^3}$
Multiply: $f"(x)=\frac{6(3-1)}{(1+1)^3}$
Subtract/Add: $f"(x)=\frac{6(2)}{(2)^3}$
Exponents: $f"(x)=\frac{6(2)}{8}$
Multiply: $f"(x)=\frac{12}{8}$
Simplify: $f"(x)=\frac{3}{2}$

This means that the graph f(x) is concave up after $x=\frac{\sqrt{3}}{3}$ .

Step 5: Identify

Since f"(x) changes concavity from positive to negative at $x=\frac{-\sqrt{3}}{3}$ and changes from negative to positive at $x=\frac{\sqrt{3}}{3}$ , then we know that the P.P.I's $x= \pm \frac{\sqrt{3}}{3}$ are actually P.I's.

Let's find what actual point on f(x) when the concavity changes.

$x=\frac{-\sqrt{3}}{3}$

Substitute in P.I into f(x): $f(\frac{-\sqrt{3}}{3} )=\frac{3}{1+(\frac{-\sqrt{3} }{3} )^2}$
Evaluate Exponents: $f(\frac{-\sqrt{3}}{3} )=\frac{3}{1+\frac{1}{3} }$
Add: $f(\frac{-\sqrt{3}}{3} )=\frac{3}{\frac{4}{3} }$
Divide: $f(\frac{-\sqrt{3}}{3} )=\frac{9}{4}$

$x=\frac{\sqrt{3}}{3}$

Substitute in P.I into f(x): $f(\frac{\sqrt{3}}{3} )=\frac{3}{1+(\frac{\sqrt{3} }{3} )^2}$
Evaluate Exponents: $f(\frac{\sqrt{3}}{3} )=\frac{3}{1+\frac{1}{3} }$
Add: $f(\frac{\sqrt{3}}{3} )=\frac{3}{\frac{4}{3} }$
Divide: $f(\frac{\sqrt{3}}{3} )=\frac{9}{4}$

Step 6: Define Intervals

We know that before f(x) reaches $x=\frac{-\sqrt{3}}{3}$ , the graph is concave up. We used the 2nd Derivative Test to confirm this.

We know that after f(x) passes $x=\frac{\sqrt{3}}{3}$ , the graph is concave up. We used the 2nd Derivative Test to confirm this.

Concave Up Interval: $(- \infty,\frac{-\sqrt{3} }{3} )U(\frac{\sqrt{3} }{3} , \infty)$

We know that after f(x) passes $x=\frac{-\sqrt{3}}{3}$ , the graph is concave up until $x=\frac{\sqrt{3}}{3}$ . We used the 2nd Derivative Test to confirm this.

Concave Down Interval: $(\frac{-\sqrt{3} }{3}, \frac{\sqrt{3} }{3} )$

6 0

3 years ago

A-b

Lynna [10]

Answer:

$\boxed{\sf d. \ \frac{a}{b} = \frac{10}{7}}$

Step-by-step explanation:

$\sf \implies \dfrac{a - b}{b} = \dfrac{3}{7} \\ \\ \sf \implies \frac{a}{b} - \frac{b}{b} = \frac{3}{7} \\ \\ \sf \implies \frac{a}{b} - 1 = \frac{3}{7} \\ \\ \sf \implies \frac{a}{b} - 1 + 1 = \frac{3}{7} + 1 \\ \\ \sf \implies \frac{a}{b} = \frac{3}{7} + 1 \\ \\ \sf \implies \frac{a}{b} = \frac{3}{7} + \frac{7}{7} \\ \\ \sf \implies \frac{a}{b} = \frac{3 + 7}{7} \\ \\ \sf \implies \frac{a}{b} = \frac{10}{7}$

6 0

3 years ago

Read 2 more answers

Aline's

const2013 [10]

Answer:

y = -1/3 + 7

Step-by-step explanation:

3 0

3 years ago

-5g-3/h-3 + 7g+9/h-3 find the sum

Licemer1 [7]

-5g - 3/h-3 + 7g +9/h-3 = -5g + 7g -3/h-3 + 9/h-3 = 2g + (9 - 3)/(h-3) =
= 2g + 6/(h-3) if we want it as one fraction it would be:

2g + 6/(h-3) = [2g(h-3) + 6]/(h-3) = $\frac{2gh - 6gh + 6}{h-3}$

5 0

3 years ago

Sanjay has 3 2/3 yards of yellow ribbon and 5 2/3 yards of blue ribbon. How many yards of ribbon does Sanjay have altogether? A.

Klio2033 [76]

This is exactly like the last question you posted. First you have to change the 3 and 2/3 mixed fraction into a pure fraction. 3 and 2/3 = 9/3 and 2/3 = 11/3 "eleven thirds." You now just need to divide (11 / 3) by (2/3.) (11 / 3) / (2 / 3) = (11 / 3) * (3 / 2) = 11 / 2 = 5 and 1/2 pieces. So if Mae cuts the ribbon into pieces that are 2/3 yard long, Mae will end up with 5 and 1/2 pieces. Checking our work, 5 pieces would be 5 * (2/3) = 10 / 3 = 3 and 1/3 yard long, leaving us with an extra 1/3 yard of ribbon, which is the "half piece" we got. Depending on the phrasing of the question, the answer could be "Mae makes 5 and a half pieces." or "Mae can make 5 pieces, and will have 1/3 yard of ribbon left over."
the answer is C. 9 1/3
Hope this helps!

6 0

4 years ago

Read 2 more answers