58): Solution =====> Letter Choice, (C) 1.25m = 1.50(m - 2)
Let's solve your equation step-by-step.
1.25m = 1.5(m − 2)
Step 1: Simplify both sides of the equation.
1.25m = 1.5(m − 2)
1.25m = (1.5)(m) + (1.5)(−2) (Distribute)
1.25m = 1.5m + −3
1.25m = 1.5m − 3
Step 2: Subtract 1.5m from both sides.
1.25m − 1.5m = 1.5m − 3 − 1.5m
−0.25m = −3
Step 3: Divide both sides by -0.25.
-0.25m/ -0.25 = -3/ -0.25
m =========> 12
Answer ===========> m = 12
59): Let your Number be: D
Solution: =====> 7D = 5D - 3 =====> -3/2 =====> -1.5
Seven Times a number:
7 * D or 7(D)
Three Less than Five Times that Number:
5D - 3
7D = 5D - 3
Solve for D:
7D = 5D - 3
Subtract 5D from both sides:
7D - 5D = 5D - 3 - 5D
2D = -3
Divide both sides by 2:
2D/2 = -3/2
D = -3/2
Answer ==> D ====> -3/2 ========> Letter Choice, (F) - 1.5
60): Letter Choice, (C), 3x - 9 = 5x
Let's solve your equation step-by-step.
3x − 9 = 5x
Step 1: Subtract 5x from both sides.
3x − 9 − 5x = 5x − 5x
−2x − 9 = 0
Step 2: Add 9 to both sides.
−2x − 9 + 9 = 0 + 9
−2x = 9
Step 3: Divide both sides by -2.
-2x/ -2 = 9/ -2
x = -9/2
Answer ========> x = -9/2 =======> 4.5
61): Subtract:
500 - 120
= 380
Need to total 500:
380
Find Number of Weeks Divide:
380/20 = 19 Weeks
7 * 19 = 133
Days it will take Nichole to save $500.00 =======> 133 Days
62): Gridded Response:
Solve:
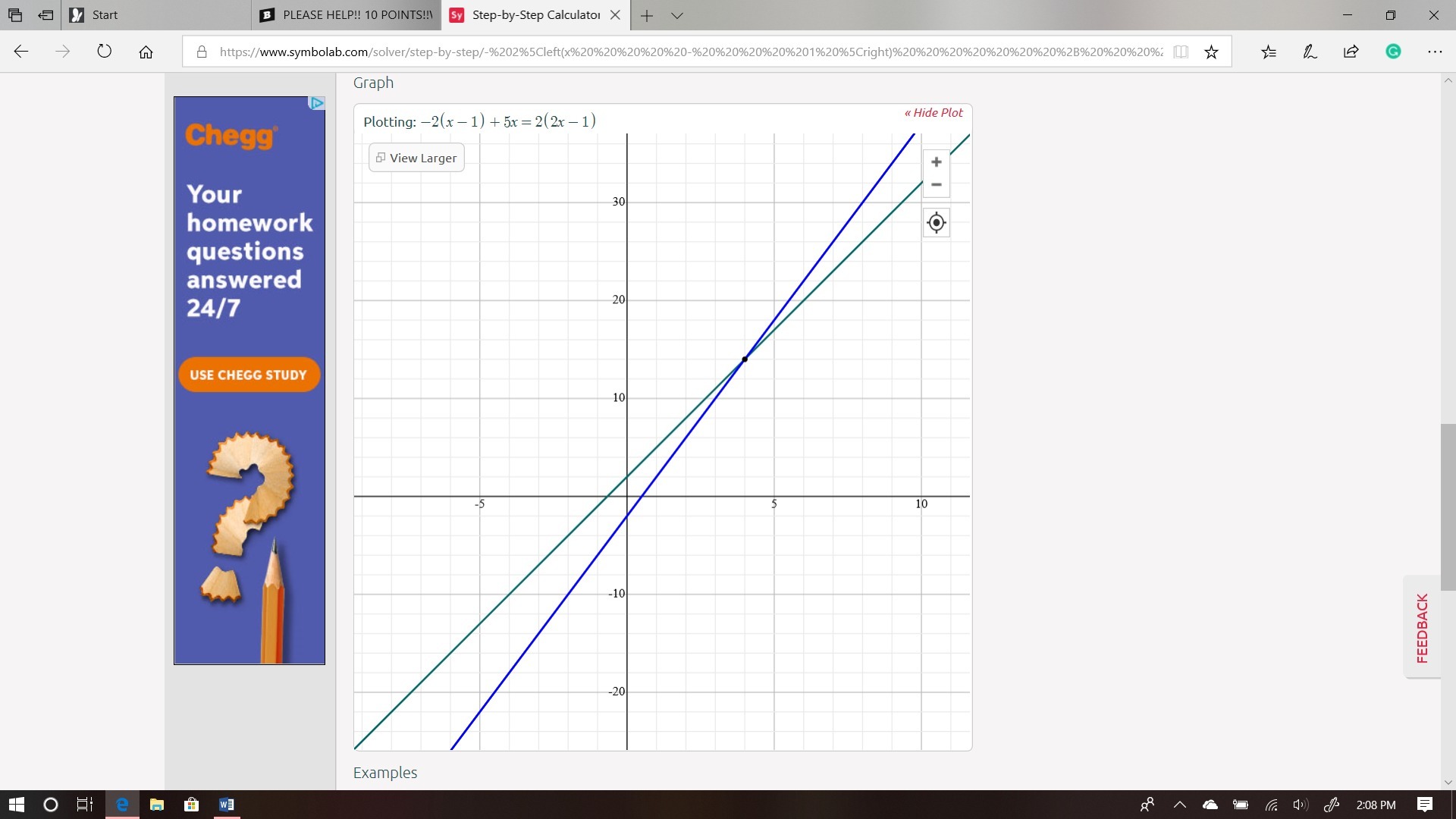
- 2(x - 1 ) + 5x = 2(2x - 1 ) ======> x = 4
( -2 )(x) + ( -2)( - 1 ) + 5x = (2)(2x) + (2)( - 1 )
Distribute:
- 2x + 2 + 5x = 4x + - 2
( - 2x + 5x ) + (2) = 4x - 2 (Combine Like terms):
3x + 2 = 4x - 2
3x + 2 = 4x - 2
Subtract 4x From both sides:
3x + 2 - 4x = 4x - 2 - 4x - x + 2 = -2
Subtract 2 from both sides:
-x + 2 - 2 = -2 - 2
-x = -4
Divide both sides by -1:
-x/ -1 = -4/ -1
x = 4
Answer =====> x = 4 Check the Graph down below for Gridded Response on Number 62.
Hope that helps!!! : ) _P_