All categories

3 years ago

A jewelry store has 311.75 ounces of 14-carat gold in stock.

Mathematics

1 answer:

WARRIOR [948]3 years ago

4 0

Answer:

$\boxed{\text{(a) 86 necklaces; (b) \$2220}}$

Step-by-step explanation:

(a) Number of necklaces

3⁵/₈ = 3.625

$\text{No. of necklaces} = 311.75\text{ oz} \times \dfrac{\text{1 necklace}}{3.625\text{ oz}} = \textbf{ 86 necklaces}\\\\\text{You can make } \boxed{\textbf{86 necklaces}} \text{ from 311.75 oz of 14K gold}$

(b) Value of gold in each necklace

There are 3.625 oz of 14K gold in each necklace. Pure gold is 24K.

$\text{Mass of pure gold} = \text{3.625 oz} \times \dfrac{\text{14K}}{\text{24K}} = \text{2.1146 oz}$

Pure 24K gold is worth $1050/oz.

$\text{Value of pure gold} = \text{2.1146 oz} \times \dfrac{\text{\$1050}}{\text{1 oz}} = \textbf{\$2220}\\\\\text{The value of the gold in each necklace is } \boxed{\textbf{\$2220}}$

You might be interested in

Help plz ASAP Find the value of x

SashulF [63]

Answer:

122

Step-by-step explanation:

6 0

3 years ago

A random sample of soil specimens was obtained, and the amount of organic matter (%) in the soil was determined for each specime

MrRissso [65]

Answer:

We conclude that the true average percentage of organic matter in such soil is something other than 3% at 10% significance level.

We conclude that the true average percentage of organic matter in such soil is 3% at 5% significance level.

Step-by-step explanation:

We are given a random sample of soil specimens was obtained, and the amount of organic matter (%) in the soil was determined for each specimen;

1.10, 5.09, 0.97, 1.59, 4.60, 0.32, 0.55, 1.45, 0.14, 4.47, 1.20, 3.50, 5.02, 4.67, 5.22, 2.69, 3.98, 3.17, 3.03, 2.21, 0.69, 4.47, 3.31, 1.17, 0.76, 1.17, 1.57, 2.62, 1.66, 2.05.

Let $\mu$ = true average percentage of organic matter

So, Null Hypothesis, 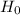$H_0$ : $\mu$ = 3% {means that the true average percentage of organic matter in such soil is 3%}

Alternate Hypothesis, $H_A$ : $\mu \neq$ 3% {means that the true average percentage of organic matter in such soil is something other than 3%}

The test statistics that will be used here is One-sample t-test statistics because we don't know about the population standard deviation;

T.S. = $\frac{\bar X-\mu}{\frac{s}{\sqrt{n} } }$ ~ $t_n_-_1$

where, $\bar X$ = sample mean percentage of organic matter = 2.481%

s = sample standard deviation = 1.616%

n = sample of soil specimens = 30

So, the test statistics = $\frac{2.481-3}{\frac{1.616}{\sqrt{30} } }$ ~ $t_2_9$

= -1.76

The value of t-test statistics is -1.76.

(a) Now, at 10% level of significance the t table gives a critical value of -1.699 and 1.699 at 29 degrees of freedom for the two-tailed test.

Since the value of our test statistics doesn't lie within the range of critical values of t, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region.

Therefore, we conclude that the true average percentage of organic matter in such soil is something other than 3% at 10% significance level.

(b) Now, at 5% level of significance the t table gives a critical value of -2.045 and 2.045 at 29 degrees of freedom for the two-tailed test.

Since the value of our test statistics lies within the range of critical values of t, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region.

Therefore, we conclude that the true average percentage of organic matter in such soil is 3% at 5% significance level.

8 0

4 years ago

The box plot shows the time it takes you and your classmates to get to school. What is the median time spent traveling to school

Vinvika [58]

B 12 minutes
Because if you look the middle of the box plot the line is at 12

5 0

3 years ago

Explain how to do (2^-2/3^3)^4 i need to know how to do this.

cricket20 [7]

Answer:

((2^(-2))÷(3^3))^4=

Step-by-step explanation: expand

5 0

3 years ago

In the smoky mountains of Tennessee, the percent of moisture that falls as snow rather than rain is approximated by P = 10.0 ln

Mars2501 [29]

Answer:

A. About 4,900 ft

Step-by-step explanation:

We want h such that ...

5 = 10·ln(h) -80

8.5 = ln(h) . . . . . . . add 80, divide by 10

e^8.5 = h ≈ 4914.8 . . . . take the antilog

h ≈ 4900 . . . . feet

7 0

4 years ago