Explanation:
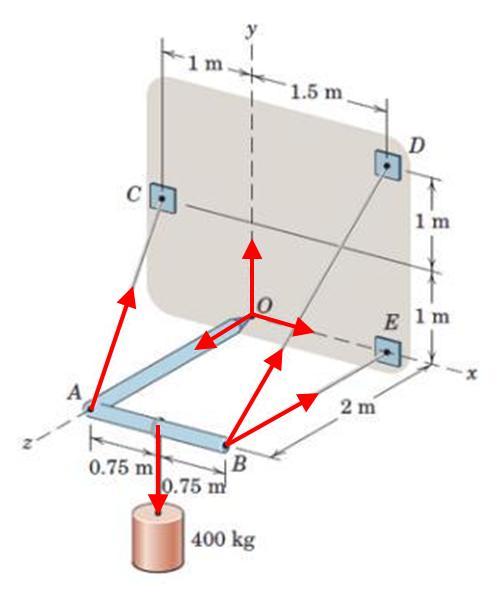
Draw a free body diagram of the bar.
There are 3 reaction forces at O in the x, y, and z direction (Ox, Oy, and Oz).
There is a tension force Tac at A in the direction of the rope. There are also tension forces Tbd and Tbe at B in the direction of the ropes.
Finally, there is a weight force mg pulling down halfway between A and B, where m = 400 kg.
There are 6 unknown variables, so we'll need 6 equations to solve. Summing the forces in the x, y, and z direction will give us 3 equations. Summing the torques about the x, y, and z axes will give us 3 more equations.
First, let's find the components of the tension forces.
Tbe is purely in the z direction.
Tbd has components in the y and z directions. The length of Tbd is √8.
(Tbd)y = 2/√8 Tbd
(Tbd)z = 2/√8 Tbd
Tac has components in the x, y, and z directions. The length of Tac is √6.
(Tac)x = 1/√6 Tac
(Tac)y = 1/√6 Tac
(Tac)z = 2/√6 Tac
Sum of the forces in the +x direction:
∑F = ma
Ox − (Tac)x = 0
Ox − 1/√6 Tac = 0
Sum of the forces in the +y direction:
∑F = ma
Oy + (Tac)y + (Tbd)y − mg = 0
Oy + 1/√6 Tac + 2/√8 Tbd − mg = 0
Sum of the forces in the +z direction:
∑F = ma
Oz − (Tac)z − (Tbd)z − Tbe = 0
Oz − 2/√6 Tac − 2/√8 Tbd − Tbe = 0
Sum of the torques counterclockwise about the x-axis:
∑τ = Iα
mg (2 m) − (Tac)y (2 m) − (Tbd)y (2 m) = 0
mg − (Tac)y − (Tbd)y = 0
mg − 1/√6 Tac − 2/√8 Tbd = 0
Sum of the torques counterclockwise about the y-axis:
∑τ = Iα
-(Tac)x (2 m) + (Tbd)z (1.5 m) + Tbe (1.5 m) = 0
-4 (Tac)x + 3 (Tbd)z + 3 Tbe = 0
-4/√6 Tac + 6/√8 Tbd + 3 Tbe = 0
Sum of the torques counterclockwise about the z-axis:
∑τ = Iα
-mg (0.75 m) + (Tbd)y (1.5 m) = 0
-mg + 2 (Tbd)y = 0
-mg + 4/√8 Tbd = 0
As you can see, by summing the torques about axes passing through O, we were able to write 3 equations independent of those reaction forces. We can solve these equations for the tension forces, then go back and find the reaction forces.
-mg + 4/√8 Tbd = 0
4/√8 Tbd = mg
Tbd = √8 mg / 4
Tbd = √8 (400 kg) (9.8 m/s²) / 4
Tbd = 2772 N
mg − 1/√6 Tac − 2/√8 Tbd = 0
1/√6 Tac = mg − 2/√8 Tbd
Tac = √6 (mg − 2/√8 Tbd)
Tac = √6 ((400 kg) (9.8 m/s²) − 2/√8 (2772 N))
Tac = 4801 N
-4/√6 Tac + 6/√8 Tbd + 3 Tbe = 0
3 Tbe = 4/√6 Tac − 6/√8 Tbd
Tbe = (4/√6 Tac − 6/√8 Tbd) / 3
Tbe = (4/√6 (4801 N) − 6/√8 (2772 N)) / 3
Tbe = 653 N
Now, using our sum of forces equations to find the reactions:
Ox − 1/√6 Tac = 0
Ox = 1/√6 Tac
Ox = 1/√6 (4801 N)
Ox = 1960 N
Oy + 1/√6 Tac + 2/√8 Tbd − mg = 0
Oy = mg − 1/√6 Tac − 2/√8 Tbd
Oy = (400 kg) (9.8 m/s²) − 1/√6 (4801 N) − 2/√8 (2772 N)
Oy = 0 N
Oz − 2/√6 Tac − 2/√8 Tbd − Tbe = 0
Oz = 2/√6 Tac + 2/√8 Tbd + Tbe
Oz = 2/√6 (4801 N) + 2/√8 (2772 N) + 653 N
Oz = 6533 N