Answer:
or P(x>49) is about 97.725% (or being less precise 97.5% using the <em>empirical rule</em>).
Step-by-step explanation:
We solve this question using the following information:
- We are dealing here with <em>normally distributed data</em>, that is "<em>the frequency distribution of the life length data is known to be mound-shaped</em>".
- The normal distribution is defined by two parameters: the population mean (
) and the population standard deviation (
). In this case, we have that
months, and
months.
- To find the probabilities, we have to use the <em>standard normal distribution</em>, which has
and
. The probabilities for this distribution are collected in the <em>standard normal table</em>, available in Statistics books or on the Internet. We can also use statistics programs to find these probabilities.
- For most cases, we need to use the <em>cumulative standard normal table, </em>and for this we have to previously "transform" a raw score (x) into a z-score using the next formula:
[1]. A z-score tells us the distance from the mean that a raw score is from it in <em>standard deviations units</em>. If this value is <em>negative</em>, the raw score is <em>below</em> the mean. Conversely, a <em>positive</em> value indicates that it is <em>above</em> the mean.
- The <em>cumulative standard normal table </em>is made for positive values of z. Since the normal distribution is <em>symmetrical</em> around the mean, we can find the negative values of z using this formula:
[2].
Having all this information, we can solve the question.
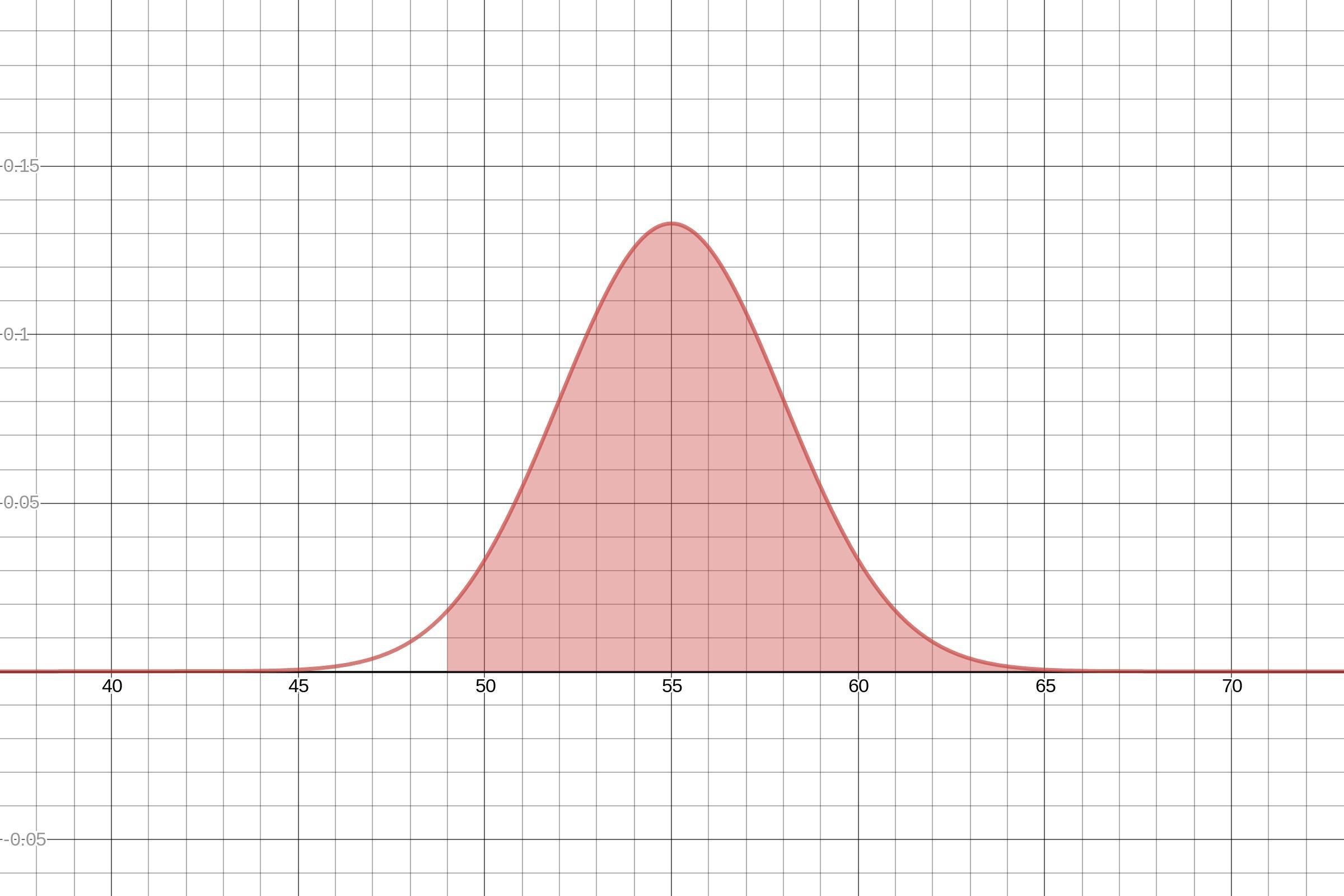
<h3>The percentage of the manufacturer's grade A batteries that will last more than 49 months</h3><em>First Step: Use formula [1] to find the z-score of the raw score x = 49 months</em>.
This means that the raw score is represented by a z-score of , which tells us that it is<em> two standard deviations below</em> the population mean.
<em>Second Step: Consult this value in the cumulative standard normal table for z = 2 and apply the formula [2] to find the corresponding probability.</em>
For a z = 2, the probability is 0.97725.
Then
But we <em>are not asked</em> for P(z<-2) but for P(z>-2) = P(x>49). This probability is the <em>complement</em> of the previous result, that is
That is, the "<em>percentage of the manufacturer's grade A batteries will last more than 49 months</em>" is
or about 97.725%
A graph below shows this result.
Notice that if we had used the <em>68-95-99.7 rule</em> (also known as the <em>empirical rule</em>), that is, in a normal distribution, the interval between <em>one standard deviation below and above the mean</em> contains, approximately, 68% of the observations; the interval between <em>two standard deviations below and above the mean</em> contains, approximately, 95% of the observations; and the interval between <em>three standard deviations</em> below and above the mean contains, approximately, 99.7% of the observations, we could have concluded that 2.5 % of the manufacturer's grade A batteries will last <em>less</em> than 49 months, and, as a result, 1 - 0.025 = 0.975 or 97.5% will last more than 49 months.
We can conclude that with a less precise answer (but faster) because of the <em>symmetry of the normal distribution</em>, that is, 1 - 0.95 = 0.05. At both extremes we have 0.05/2 = 0.025 or 2.5% and we were asked for P(x>49) = P(z>-2) (see the graph below).