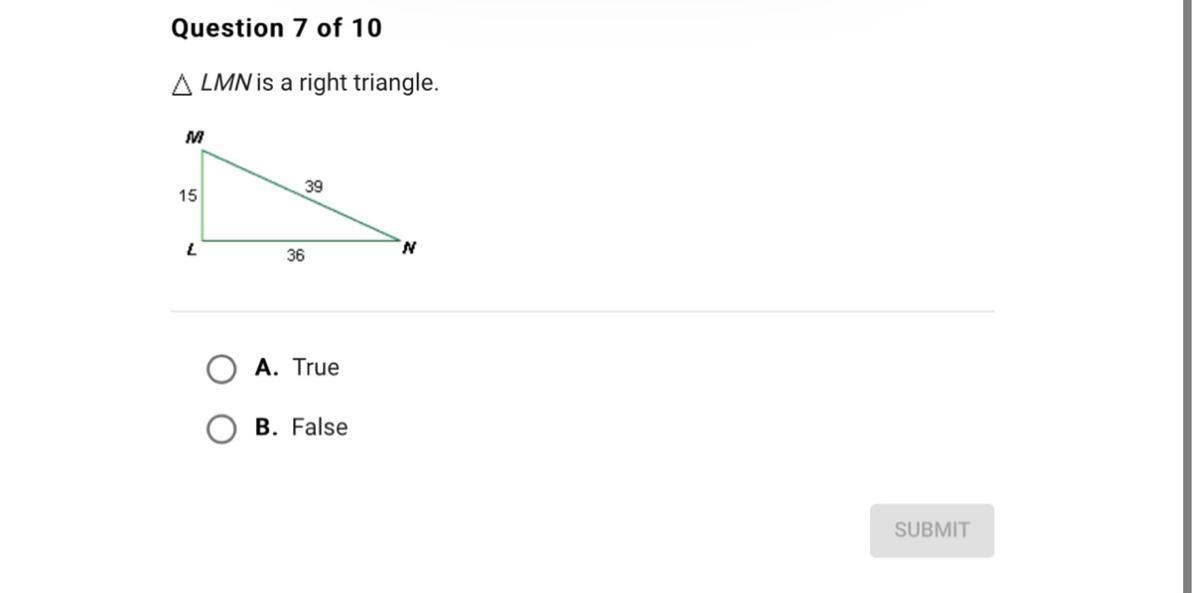
Answer:
The trick I’d like to share gives you and your children a fast way to find the Least Common Multiple (LCM). FYI, the LCM is also called the LCD (Least Common Denominator) in problems requiring students to find a common denominator. So in this article I will use the two terms and abbreviations interchangeably.
When tutoring students working with fractions, I often see kids stressed while trying to find the LCD for two numbers. For example, in solving 3/16 + 11/24, I see kids pulling their hair out, trying to find the smallest number that 16 and 24 both divide into evenly. They need to do this, of course, so that they can add the two fractions, since they need a common denominator.
It turns out that there’s a quick-and-easy technique for doing this that most people have never heard of. This technique depends on knowing how to get the GCF (Greatest Common Factor) for the same numbers, but I’ll cover that in next month’s article, and show that there’s a trick for that as well.
Back to the LCM, here’s the quick-and-easy way to find it.
1st) Find the GCF for your two denominators. In our example of 3/16 + 11/24, the denominators are 16 and 24, and their GCF is 8.
2nd) Choose one of the two denominators. It doesn’t matter which one you pick .So we’ll just choose the first one listed, 16.
3rd) Divide the denominator you picked by the GCF. 16 ÷ 8 = 2.
4th) Take the quotient you just got, 2, and multiply it by the other denominator, 24. That gives you: 2 x 24 = 48. And voilà! This means that 48 is the Least Common Denominator for 16 and 24. Try it and see: 16 divides into 48 three times; 24 divides into 48 twice. So that means that for this fraction addition problem, the LCD = 48,. Once your children know that, they can easily convert and add the fractions.
Just to make sure that everyone gets the idea, let’s try this same process in another problem. Suppose your child is working the fraction subtraction problem: 37/45 – 11/25. First she needs to find the LCD for the denominators of 45 and 25. Seems tough, right? But watch, again, how these simple steps make quick work of this part of the problem.
1st) Find the GCF for 45 and 25. That would be 5.
2nd) Choose either denominator. It doesn’t matter which one you pick, so we’ll arbitrarily choose 45.
3rd) Divide the denominator you just chose by the GCF. 45 ÷ 5 = 9.
4th) Take the answer you just got, 9, and multiply it by the other denominator, 25.
9 x 25 = 225. So 225 is the LCM for 45 and 25.
Check it to see. 45 divides evenly into 225, five times; likewise, 25 divides evenly into 225, nine times. So once again, this trick allows children to find the LCM with a minimum of effort. And after all, math is more fun when you can work with numbers quickly and efficiently.
Anyone wondering why this “trick” works? It is based on a fundamental concept of Number Theory, a theorem that states: GIVEN ANY TWO WHOLE NUMBERS, THE PRODUCT OF THOSE NUMBERS EQUALS THE PRODUCT OF THEIR LCM AND GCF. Or, in more simple English. If you multiply any two whole numbers together, the number you get is the same as what you get when you multiply the LCM and GCF of those numbers together.
Take the first example, and you’ll see that this is true. The numbers are 16 and 24. 16 x 24 = 384. And for 16 and 24, the GCF = 8, and the LCM = 48. And 8 x 48 = 384.
Now to see how this theorem provides a foundation for the LCM trick, examine this quick argument.
Call any two whole numbers N1 and N2. Call the GCF for these numbers “G”; call their LCM “L.”
This theorem states: N1 x N2 = G x L
That being true, we can flip the equation around: G x L = N1 x N2.
Next divide both sides by G, like this: (G x L) ÷ G = (N1 x N2) ÷ G
Seeing that G ÷ G = 1 on the left side, the equation becomes: L = (N1 x N2) ÷ G
Next just re-arrange the right side, like this: L = (N1 ÷ G) x N2
And there you have it. For this says that the LCM (L) is equal to one of the numbers (N1) divided by the GCF (G), and then that quotient multiplied by the other number (N2). Pretty nifty, huh?
As a follow-up, here’s a chance to practice this trick. Below you will find ten pairs of numbers. All you need to do is follow the steps I’ve laid out to find the LCM for each pair of numbers. The answers follow the problems.
PROBLEMS:
a) 6 and 8
b) 4 and 10
c) 9 and 15
d) 10 and 16
e) 14 and 21
f) 18 and 45
g) 24 and 28
h) 27 and 63
i) 32 and 48
j) 45 and 55
ANSWERS:
a) 6 and 8; GCF = 2; LCM = 24
b) 4 and 10; GCF = 2; LCM = 20
c) 9 and 15; GCF = 3; LCM = 45
d) 10 and 16; GCF = 2; LCM = 80
e) 14 and 21; GCF = 7; LCM = 42
f) 18 and 45; GCF = 9; LCM = 90
g) 24 and 28; GCF = 4; LCM = 168
h) 27 and 63; GCF = 9; LCM = 189
i) 32 and 48; GCF = 16; LCM = 96
j) 45 and 55; GCF = 5; LCM = 495
Step-by-step explanation: