All categories

3 years ago

What happens to the focal length of a converging lens when it is placed under water?

Physics

2 answers:

IceJOKER [234]3 years ago

7 0

Answer:

When a converging lens is placed under water then its focal length increases.

Explanation:

When any lens, be it converging or diverging is immersed into water then the speed of light before and after the refraction through the lens has less speed and due to less difference in speed it shows less deviations as a result the focal length is increased for the lenses.

Lesser the difference between the refractive index of the medium and the lens glass greater becomes its focal length.

<u>The focal length of the lens immersed in a medium is given by:</u>

$\frac{1}{f} =\frac{n_l-n_m}{n_m} \times (\frac{1}{R_1} +\frac{1}{R_2} )$

where:

$n_l=$ refractive index of the glass material with resp. to air

$n_m=$ refractive index of the medium with resp. to air

$R_1\ \&\ R_2=$ radii of curvature of the two surfaces of the lens

alisha [4.7K]3 years ago

3 0

Answer:

Explanation:

According to the lens maker's formula

The focal length of the converging lens in air is given by

$\frac{1}{f_{a}}=\left ( \mu _{a}-1 \right )\left ( \frac{1}{R_{1}}-\frac{1}{R_{2}} \right )$ .... (1)

Where, R1 and R2 be the radius of curvature of the lens and μa is the refractive index of glass in air.

When the lens is placed in water. the focal length is given by

$\frac{1}{f_{w}}=\left ( \frac{\mu _{a}}{\mu _{w}}-1 \right )\left ( \frac{1}{R_{1}}-\frac{1}{R_{2}} \right )$ .... (2)

Where, R1 and R2 be the radius of curvature of the lens and μa is the refractive index of lens in air and μw is the refractive index of glass in water.

Dividing equation (1) by (2), we observe that the value of focal length,

the focal length of lens in water increases.

You might be interested in

A) In the figure below, a cylinder is compressed by means of a wedge against an elastic constant spring = 12 /. If = 500 , deter

Radda [10]

Explanation:

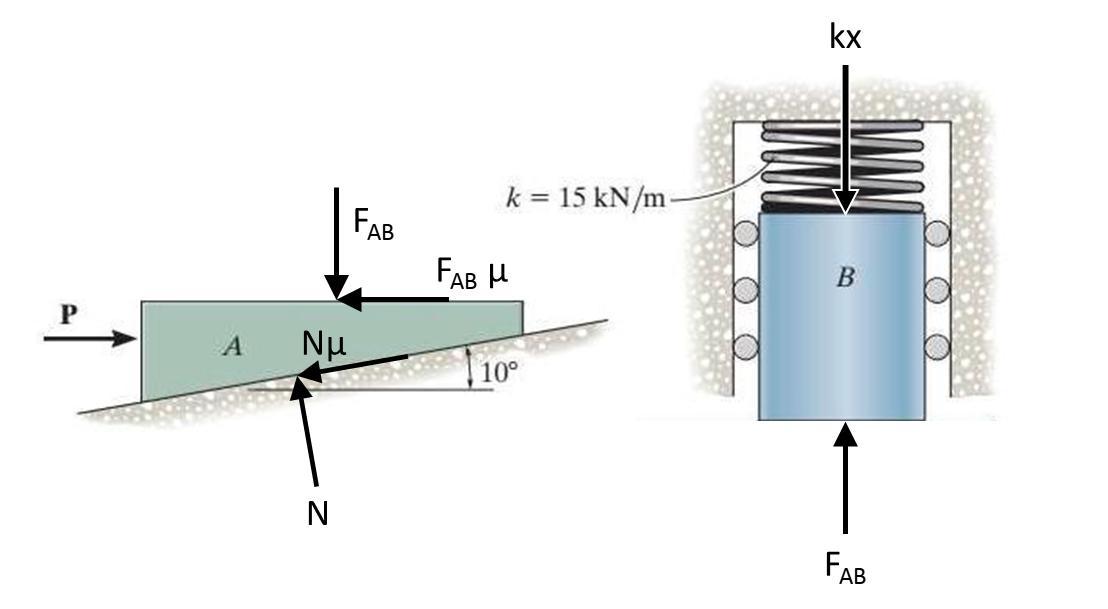
A) Draw free body diagrams of both blocks.

Force P is pushing right on block A, which will cause it to move right along the incline. Therefore, friction forces will oppose the motion and point to the left.

There are 5 forces acting on block A:

Applied force P pushing to the right,

Normal force N pushing up and left 10° from the vertical,

Friction force Nμ pushing down and left 10° from the horizontal,

Reaction force Fab pushing down,

and friction force Fab μ pushing left.

There are 2 forces acting on block B:

Reaction force Fab pushing up,

And elastic force kx pushing down.

(There are also horizontal forces on B, but I am ignoring them.)

Sum of forces on A in the x direction:

∑F = ma

P − N sin 10° − Nμ cos 10° − Fab μ = 0

Solve for N:

P − Fab μ = N sin 10° + Nμ cos 10°

P − Fab μ = N (sin 10° + μ cos 10°)

N = (P − Fab μ) / (sin 10° + μ cos 10°)

Sum of forces on A in the y direction:

N cos 10° − Nμ sin 10° − Fab = 0

Solve for N:

N cos 10° − Nμ sin 10° = Fab

N (cos 10° − μ sin 10°) = Fab

N = Fab / (cos 10° − μ sin 10°)

Set the expressions equal:

(P − Fab μ) / (sin 10° + μ cos 10°) = Fab / (cos 10° − μ sin 10°)

Cross multiply:

(P − Fab μ) (cos 10° − μ sin 10°) = Fab (sin 10° + μ cos 10°)

Distribute and solve for Fab:

P (cos 10° − μ sin 10°) − Fab (μ cos 10° − μ² sin 10°) = Fab (sin 10° + μ cos 10°)

P (cos 10° − μ sin 10°) = Fab (sin 10° + 2μ cos 10° − μ² sin 10°)

Fab = P (cos 10° − μ sin 10°) / (sin 10° + 2μ cos 10° − μ² sin 10°)

Sum of forces on B in the y direction:

∑F = ma

Fab − kx = 0

kx = Fab

x = Fab / k

x = P (cos 10° − μ sin 10°) / (k (sin 10° + 2μ cos 10° − μ² sin 10°))

Plug in values and solve.

x = 500 N (cos 10° − 0.4 sin 10°) / (12000 (sin 10° + 0.8 cos 10° − 0.16 sin 10°))

x = 0.0408 m

x = 4.08 cm

B) Draw free body diagrams of both blocks.

Force P is pushing block A to the right relative to the ground C, so friction force points to the left.

Block A moves right relative to block B, so friction force on A will point left. Block B moves left relative to block A, so friction force on B will point right (opposite and equal).

Block B moves up relative to the wall D, so friction force on B will point down.

There are 5 forces acting on block A:

Applied force P pushing to the right,

Normal force Fc pushing up,

Friction force Fc μ₁ pushing left,

Reaction force Fab pushing down and left 15° from the vertical,

and friction force Fab μ₂ pushing up and left 15° from the horizontal.

There are 5 forces acting on block B:

Weight force 750 n pushing down,

Normal force Fd pushing left,

Friction force Fd μ₁ pushing down,

Reaction force Fab pushing up and right 15° from the vertical,

and friction force Fab μ₂ pushing down and right 15° from the horizontal.

Sum of forces on B in the x direction:

∑F = ma

Fab μ₂ cos 15° + Fab sin 10° − Fd = 0

Fd = Fab μ₂ cos 15° + Fab sin 15°

Sum of forces on B in the y direction:

∑F = ma

-Fab μ₂ sin 15° + Fab cos 10° − 750 − Fd μ₁ = 0

Fd μ₁ = -Fab μ₂ sin 15° + Fab cos 15° − 750

Substitute:

(Fab μ₂ cos 15° + Fab sin 15°) μ₁ = -Fab μ₂ sin 15° + Fab cos 15° − 750

Fab μ₁ μ₂ cos 15° + Fab μ₁ sin 15° = -Fab μ₂ sin 15° + Fab cos 15° − 750

Fab (μ₁ μ₂ cos 15° + μ₁ sin 15° + μ₂ sin 15° − cos 15°) = -750

Fab = -750 / (μ₁ μ₂ cos 15° + μ₁ sin 15° + μ₂ sin 15° − cos 15°)

Sum of forces on A in the y direction:

∑F = ma

Fc + Fab μ₂ sin 15° − Fab cos 15° = 0

Fc = Fab cos 15° − Fab μ₂ sin 15°

Sum of forces on A in the x direction:

∑F = ma

P − Fab sin 15° − Fab μ₂ cos 15° − Fc μ₁ = 0

P = Fab sin 15° + Fab μ₂ cos 15° + Fc μ₁

Substitute:

P = Fab sin 15° + Fab μ₂ cos 15° + (Fab cos 15° − Fab μ₂ sin 15°) μ₁

P = Fab sin 15° + Fab μ₂ cos 15° + Fab μ₁ cos 15° − Fab μ₁ μ₂ sin 15°

P = Fab (sin 15° + (μ₁ + μ₂) cos 15° − μ₁ μ₂ sin 15°)

First, find Fab using the given values.

Fab = -750 / (0.25 × 0.5 cos 15° + 0.25 sin 15° + 0.5 sin 15° − cos 15°)

Fab = 1151.9 N

Now, find P.

P = 1151.9 N (sin 15° + (0.25 + 0.5) cos 15° − 0.25 × 0.5 sin 15°)

P = 1095.4 N

6 0

3 years ago

The animal that is hunted and consumed is considered the

KatRina [158]

The animal that is hunted and consumed is considered the prey

4 0

3 years ago

Read 2 more answers

Which objects have both potential and kinetic energy? Check all that apply.

wariber [46]

A falling raindrop
Kinetic energy and potential energy are both applied when a body or object is falling.

3 0

4 years ago

Read 2 more answers

__________ is a type of molding in which thermoplastics are heated above melting temperature and, using an extruder, are forced

Ymorist [56]

Answer: The correct and is

D. Extrusion

Explanation:

What is extrusion?

Extrusion is a manufacturing process used to make basically pipes and hoses.

The pvc granules are melt into a liquid which is forced through a die, forming a long 'tube like' shape. The shape of the die determines the shape of the tube.

The extrusion is then cooled and forms a solid shape

Extrusion moulding is used to create products with a consistent cross-section.

4 0

3 years ago

A small sphere with mass mcarries a positive chargeqand is attached to one end of a silk fiber of lengthL. The other end of the

Aleksandr-060686 [28]

Answer:

(a): The magnitude of the electric force on the small sphere = $\dfrac{q\sigma}{2\epsilon_o}.$

(b): Shown below.

Explanation:

<u>Given:</u>

m = mass of the small sphere.
q = charge on the small sphere.
L = length of the silk fiber.
$\sigma$ = surface charge density of the large vertical insulating sheet.

When the dimensions of the sheet is much larger than the distance between the charge and the sheet, then, according to Gauss' law of electrostatics, the electric field experienced by the particle due to the sheet is given as:

$\rm E = \dfrac{\sigma}{2\epsilon_o}.$

<em>where,</em>

$\epsilon_o$ is the electrical permittivity of the free space.

The electric field at a point is defined as the amount of electric force experienced by a unit positive test charge, placed at that point. The magnitude electric field at a point and the magnitude of the electric force on a charge q placed at that point are related as:

$\rm F_e=qE.$

Thus, the magnitude of the electric force on the small sphere is given by

$\rm F_e = q\times \dfrac{\sigma }{2\epsilon_o}=\dfrac{q\sigma}{2\epsilon_o}.$

The sheet and the small sphere both are positively charged, therefore, the electric force between these two is repulsive, which means, the direction of the electric force on the sphere is away from the sheet along the line which is perepndicular to the sheet and joining the sphere.

When the sphere is in equilibrium, the tension in the fiber is given by the resultant of the weight of the sphere and the electric force experienced by it as shown in the figure attached below.

According to the fig.,

$\rm \tan \theta = \dfrac{F_e}{W}.$

<em>where,</em>

$\rm F_e$ = electric force on the sphere, acting along left.
$\rm W$ = weight of the sphere, acting vertically downwards.

<em />

$\rm F_e = \dfrac{q\sigma}{2\epsilon_o}\\\\W=mg\\\\Therefore,\\\\\tan\theta = \dfrac{\dfrac{q\sigma}{2\epsilon_o}}{mg}=\dfrac{q\sigma}{2mg\epsilon_o}.\\\Rightarrow \theta=\tan^{-1}\left ( \dfrac{q\sigma}{2mg\epsilon_o}\right ) .$

g is the acceleration due to gravity.

6 0

4 years ago