Answer:
a) T_1 = 938 K , T_2 = 931 K
b) To prevent softening of the materials, which would occur below their melting points, the reactor should not be operated much above:
q = 3*10^8 W/m^3
Explanation:
Given:
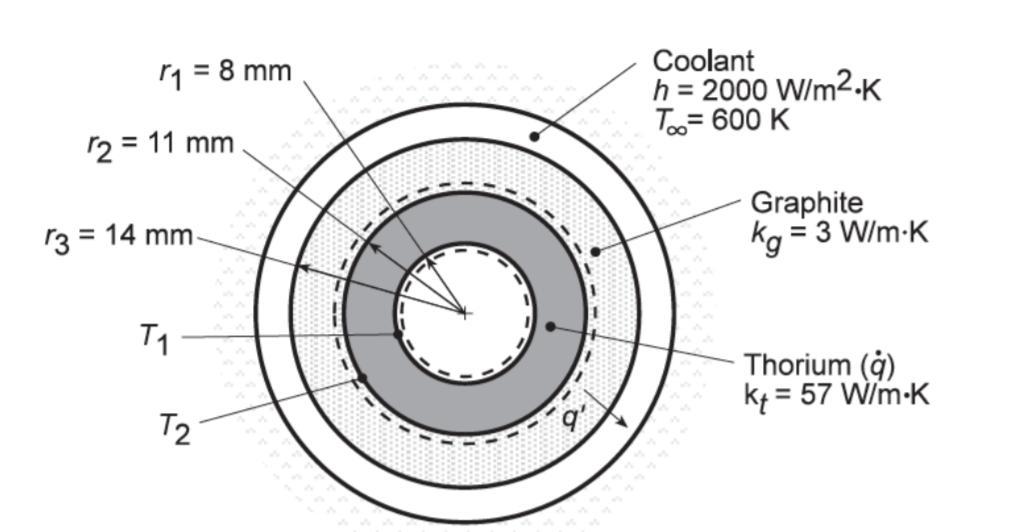
- See the attachment for the figure for this question.
- Melting point of Thorium T_th = 2000 K
- Melting point of Thorium T_g = 2300 K
Find:
a) If the thermal energy is uniformly generated in the fuel element at a rate q = 10^8 W/m^3 then what are the temperatures T_1 and T_2 at the inner and outer surfaces, respectively, of the fuel element?
b) Compute and plot the temperature distribution in the composite wall for selected values of q. What is the maximum allowable value of q.
Solution:
part a)
- The outer surface temperature of the fuel, T_2, may be determined from the rate equation:
q*A_th = T_2 - T_inf / R'_total
Where,
A_th: Area of the thorium section
T_inf: The temperature of coolant = 600 K
R'_total: The resistance per unit length.
- Calculate the resistance per unit length R' from thorium surface to coolant:
R'_total = Ln(r_3/r_2) / 2*pi*k_g + 1 / 2*pi*r_3*h
Plug in values:
R'_total = Ln(14/11) / 2*pi*3 + 1 / 2*pi*0.014*2000
R'_total = 0.0185 mK / W
- And the heat rate per unit length may be determined by applying an energy balance to a control surface about the fuel element. Since the interior surface of the element is essentially adiabatic, it follows that:
q' = q*A_th = q*pi*(r_2^2 - r_1^2)
q' = 10^8*pi*(0.011^2 - 0.008^2) = 17,907 W / m
Hence,
T_2 = q' * R'_total + T_inf
T_2 = 17,907*0.0185 + 600
T_2 = 931 K
- With zero heat flux at the inner surface of the fuel element, We will apply the derived results for boundary conditions as follows:
T_1 = T_2 + (q*r_2^2/4*k_th)*( 1 - (r_1/r_2)^2) - (q*r_1^2/2*k_th)*Ln(r_2/r_1)
Plug values in:
T_1 = 931+(10^8*0.011^2/4*57)*( 1 - (.8/1.1)^2) - (10^8*0.008^2/2*57)*Ln(1.1/.8)
T_1 = 931 + 25 - 18 = 938 K
part b)
The temperature distributions may be obtained by using the IHT model for one-dimensional, steady state conduction in a hollow tube. For the fuel element (q > 0), an adiabatic surface condition is prescribed at r_1 while heat transfer from the outer surface at r_2 to the coolant is governed by the thermal resistance:
R"_total = 2*pi*r_2*R'_total
R"_total = 2*pi*0.011*0.0185 = 0.00128 m^2K/W
- For the graphite ( q = 0 ), the value of T_2 obtained from the foregoing solution is prescribed as an inner boundary condition at r_2, while a convection condition is prescribed at the outer surface (r_3).
- For 5*10^8 < q and q > 5*10^8, the distributions are given in attachment.
The graphs obtained:
- The comparatively large value of k_t yields small temperature variations across the fuel element, while the small value of k_g results in large temperature variations across the graphite.
Operation at q = 5*10^8 W/^3 is clearly unacceptable, since the melting points of thorium and graphite are exceeded and approached, respectively. To prevent softening of the materials, which would occur below their melting points, the reactor should not be operated much above:
q = 3*10^8 W/m^3