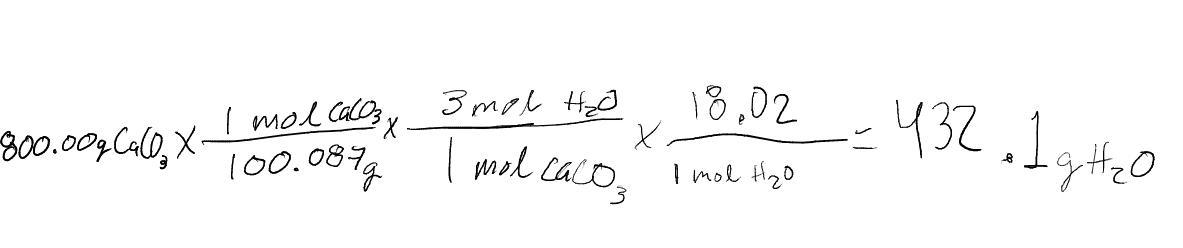Answer:
1. 10 moles of NO
2. 25 moles of NaCl
3. 1200 moles CO₂
4. 1.042 mole of MgO
5. 0.714 moles H₂ gas
6. 1040 g of BaCl₂
7. 9.5 g
8. 45.44 g of Au
9. 15 g of AlCl₃
Explanation:
Ans 1.
Data Given:
moles of Oxygen = 5 moles
moles of nitrogen monoxide = ?
Solution:
To solve this problem we have to look at the reaction
Reaction:
N₂ + O₂ -----------> 2NO
1 mol 2 mol
So if we look at the reaction 1 mole Oxygen (O₂) gives 2 moles of nitrogen monoxide NO, then how many moles of nitrogen monoxide will be produced by 5 moles of Oxygen (O₂)
For this apply unity formula
1 mole of O₂ ≅ 2 moles of NO
5 mole of O₂ ≅ X moles of NO
By Doing cross multiplication
moles of NO = 2 moles x 5 moles / 1 mole
moles of NO = 10 mole
5 mole of O₂ will produce 10 moles of NO
________________
Ans 2.
Data Given:
moles of HCl = 25 moles
moles of NaCl = ?
Solution:
To solve this problem we have to look at the reaction
Neutralization Reaction:
HCl + NaOH -----------> NaCl + H₂O
1 mol 1 mol
So if we look at the reaction 1 mole HCl gives 1 moles of NaCl, then how many moles of NaCl will be formed by 25 moles of HCl
For this apply unity formula
1 mole of HCl ≅ 1 moles of NaCl
25 mole of HCl ≅ X moles of NaCl
By Doing cross multiplication
moles of NaCl = 1 moles x 25 moles / 1 mole
moles of NaCl = 25 mole
25 mole of HCL will form 25 moles of NaCl
________________
Ans 3.
Data Given:
moles of C₈H₁₈ = 150 moles
moles of CO₂= ?
Solution:
To solve this problem we have to look at the reaction
Reaction:
2C₈H₁₈ + 25O₂ -----------> 16CO₂ + 18H₂O
2 mol 16 mol
So if we look at the reaction 2 mole C₈H₁₈ gives 16 moles of CO₂, then how many moles of CO₂ will be Produce by 150 moles of C₈H₁₈
For this apply unity formula
2 mole of C₈H₁₈ ≅ 16 moles of CO₂
150 mole of C₈H₁₈ ≅ X moles of CO₂
By Doing cross multiplication
moles of CO₂= 16 moles x 150 moles / 2 mole
moles of CO₂ = 1200 mole
150 mole of C₈H₁₈ will form 1200 moles of CO₂
______________________
Ans 4.
Data Given:
mass of Mg = 25 g
moles of MgO= ?
Solution:
To solve this problem we have to look at the reaction
Reaction:
2Mg + O₂ -----------> 2MgO
2 mol 2 mol
Convert moles of Mg to mass
Molar mass of Mg = 24 g/mol
So,
2Mg + O₂ -----------> 2MgO
2 mol (24 g/mol) 2 mol
48 g 2 mol
So if we look at the reaction 48 g of Mg gives 2 moles of MgO, then how many moles of MgO will be Produce by 25 g of Mg
For this apply unity formula
48 g of Mg ≅ 2 moles of MgO
25 g of Mg ≅ X moles of MgO
By Doing cross multiplication
moles of MgO = 2 moles x 25 g / 48 g
moles of MgO = 1.042 mole
25 g of Mg will form 1.042 moles of MgO
______________________
Ans 5.
Data Given:
mass of Li = 10 g
moles of H₂= ?
Solution:
To solve this problem we have to look at the reaction
Reaction:
2Li + 2 H₂O -----------> 2LiOH + H₂
2 mol 1 mol
Convert moles of Li to mass
Molar mass of Li = 7 g/mol
So,
2Li + 2H₂O -----------> 2LiOH + H₂
2 mol (7 g/mol) 1 mol
14 g 1 mol
So if we look at the reaction 14 g of Li gives 1 moles of H₂ gas, then how many moles of H₂ gas will be Produce by 10 g of Li
For this apply unity formula
14 g of Li ≅ 1 moles of H₂
10 g of Li ≅ X moles of H₂
By Doing cross multiplication
moles of H₂ = 1 moles x 10 g / 14 g
moles of H₂ = 0.714 mole
10 g of Li will form 0.714 moles of H₂
______________________
Ans 6.
Data Given:
moles of Na₂SO₄= 5 moles
mass of BaCl₂ = ?
Solution:
To solve this problem we have to look at the reaction
Reaction:
Na₂SO₄ + BaCl₂ -----------> 2NaCl + BaSO₄
1 mol 1 mol
Convert moles of BaCl₂ to mass
Molar mass of BaCl₂ = 208 g/mol
So,
Na₂SO₄ + BaCl₂ -----------> 2NaCl + BaSO₄
1 mol 1 mol (208 g/mol)
1 mol 208 g
So if we look at the reaction 1 mole of Na₂SO₄ react with 208 g of BaCl₂, Then how many grams of BaCl₂ will react with 5 moles of Na₂SO₄
For this apply unity formula
1 mole of Na₂SO₄ ≅ 208 g of BaCl₂
5 mole of Na₂SO₄≅ X g of BaCl₂
By Doing cross multiplication
mass of BaCl₂ = 208 g x 5 moles / 1 mole
mass of BaCl₂ = 1040 g
5 moles of Na₂SO₄ will react with 1040 g of BaCl₂
______________________
Ans 7.
Data Given:
mass of MgCO₃ = 20 g
moles of MgO= ?
Solution:
To solve this problem we have to look at the reaction
Reaction:
MgCO₃ -----------> MgO + CO₂
1 mol 1 mol
Convert moles to mass
Molar mass of MgCO₃ = 84 g/mol
Molar mass of MgO = 40 g/mol
So,
MgCO₃ -------------> MgO + CO₂
1 mol (84 g/mol) 1 mol (40 g/mol)
84 g 40 g
So if we look at the reaction 84 g of MgCO₃ gives 40 g of MgO, then how many g of MgO will be Produce by 20 g of MgCO₃
For this apply unity formula
84 g of MgCO₃ ≅ 40 g of MgO
20 g of MgCO₃ ≅ X g of MgO
By Doing cross multiplication
mass of MgO = 40 g x 20 g / 84g
mass of MgO = 9.5 g
20 g of MgCO₃ will produce 9.5 g of MgO
________________
The remaining portion is in attachment