Answer:
The complete answer along with step by step explanation and output results is provided below.
Explanation:
Task a)
#include<iostream>
using namespace std;
int main()
{
int op;
double num1, num2;
cout<<"Enter num1 and num2"<<endl;
cin>>num1>>num2;
// To provide the option of required 5 cases
cout << "Select the operation:"
"\n1 = Addition"
"\n2 = Subtraction"
"\n3 = Multiplication"
"\n4 = Division"
"\n5 = Negation\n";
cin >> op; // user input the desired operation
switch(op) // switch to the corresponding case according to user input
{
case 1:
cout <<"The Addition of num1="<<num1<<" and num2="<<num2<<" is: "<<num1+num2;
break;
case 2:
cout <<"The Subtraction of num1="<<num1<<" and num2="<<num2<<" is: "<<num1-num2;
break;
case 3:
cout <<"The Multiplication of num1="<<num1<<" and num2="<<num2<<" is: "<<num1*num2;
break;
case 4:
while(num2 == 0) // to check if divisor is zero
{
cout << "\nWrong divisor! Please select the correct divisor again: ";
cin >> num2; // if divisor is zero then ask user to input num2 again
}
cout <<"The division of num1="<<num1<<" and num2="<<num2<<" is: "<<num1/num2;
break;
case 5:
cout <<"The Negation of num1="<<num1<<" and num2="<<num2<<" is: "<<-1*num1<<" "<<-1*num2;
break;
default:
// If the operation is other than listed above then error will be shown
cout << "Error! The selected operatorion is not correct";
break;
}
return 0;
}
Output:
Test 1:
Enter num1 and num2
2
9
Select the operation:
1 = Addition
2 = Subtraction
3 = Multiplication
4 = Division
5 = Negation
1
The Addition of num1=2 and num2=9 is: 11
Hence the output is correct and working as it was required
Test 2:
Enter num1 and num2
8
0
Select the operation:
1 = Addition
2 = Subtraction
3 = Multiplication
4 = Division
5 = Negation
4
Wrong divisor! Please select the correct divisor again: 2
The Division of num1=8 and num2=2 is: 4
Hence the output is correct and working as it was required
Test 3:
Enter num1 and num2
-2
4
Select the operation:
1 = Addition
2 = Subtraction
3 = Multiplication
4 = Division
5 = Negation
5
The Negation of num1=-2 and num2=4 is: 2 -4
Hence the output is correct and working as it was required
Task b)
#include<iostream>
#include<cmath> // required to calculate square root
using namespace std;
int main()
{
int op;
double num;
cout<<"Enter a real number > 0"<<endl;
cin>>num;
cout << "Press 1 for square root:";
cin >> op;
switch(op) // switch to the corresponding case according to user input
{
case 1:
if (num <= 0) // to check if number is less or equal to zero
{
cout << "\nError! number is not valid";
break; // if number is not valid then terminate program
}
cout <<"The square root of num="<<num<<" is: "<<sqrt(num);
// if number is valid then square root will be calculated
break;
default:
// If the operation is other than listed above then error will be shown
cout << "Error! The selected operation is not correct";
break;
}
return 0;
}
Output:
Test 1:
Enter a real number > 0
6
Press 1 for square root: 1
The square root of num=6 is: 2.44949
Hence the output is correct and working as it was required
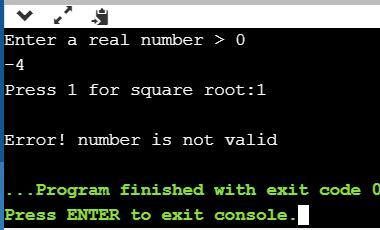
Test 2:
Enter a real number > 0
-4
Press 1 for square root: 1
Error! number is not valid
Hence the output is correct and working as it was required