Answer:
The direction of angular velocity and angular momentum are perpendicular to the plane of rotation. Using the right hand rule, the direction of both angular velocity and angular momentum is defined as the direction in which the thumb of your right hand points when you curl your fingers in the direction of rotation.
Explanation:
You can use photo math for This
The outward push of the core created by nuclear fusion and the inward pull of gravity from the core
Answer:
a. the time required for the onset of evaporation is: 196.1 seconds and b. the time required for all of the water to evaporate is: 1328.3 seconds.
Explanation:
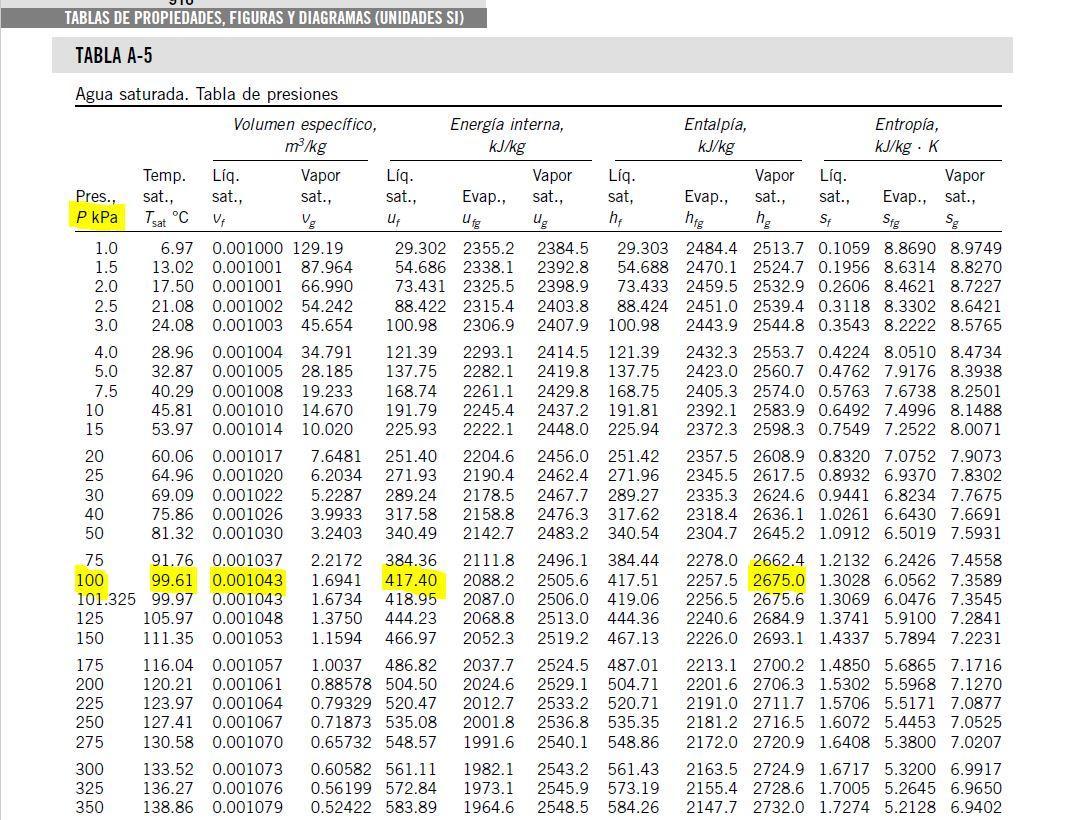
We need to stablish that there is 3 states at this problem. At the firts one, water is compressed liquid and the conditions for this state are: P1=100KPa,T1=20°C,V1=0.5m^3. From the compressed liquid chart and using extrapolation, we can get: v1=vf1=0.0010018 (m^3/Kg) and u1=uf1=83.95(KJ/kg). Now we can find the mass of water at the state 1 as:  Then the liquid water is heated at a rate of 0.85KW, and its volume increase, while work is done by the system at the boundary, we can assume that the pressure remains constant throughout the entire process. At the second state the water is saturated liquid and the conditions are: P2=100KPa, T2=Tsat=99.63°C, v2=vf2=0.001043(m^3/Kg) and u2=uf2=417.36(KJ/Kg). Now we can find the work as:
Then the liquid water is heated at a rate of 0.85KW, and its volume increase, while work is done by the system at the boundary, we can assume that the pressure remains constant throughout the entire process. At the second state the water is saturated liquid and the conditions are: P2=100KPa, T2=Tsat=99.63°C, v2=vf2=0.001043(m^3/Kg) and u2=uf2=417.36(KJ/Kg). Now we can find the work as: . (a) After that we need to do an energy balance for process 1-2 and get: U=Q-W or
. (a) After that we need to do an energy balance for process 1-2 and get: U=Q-W or  , solving for t we get the time required for the onset of evaporation:
, solving for t we get the time required for the onset of evaporation: .(b) Then continue heat transfer to the cooking pot and results in phase change getting vapor at 99.63°C. At the final state or third state the mass is zero because all liquid was evaporated and the initial mass at this state is the same for the second state: 0.5 (Kg) and doing an energy balances results in:
.(b) Then continue heat transfer to the cooking pot and results in phase change getting vapor at 99.63°C. At the final state or third state the mass is zero because all liquid was evaporated and the initial mass at this state is the same for the second state: 0.5 (Kg) and doing an energy balances results in: , but m3=0, now solving for t we can get the time required for all of the water to evaporate as:
, but m3=0, now solving for t we can get the time required for all of the water to evaporate as: . We can get from the saturated liquid chart the enthalpy he=hge=2675.5(KJ/Kg) @P=100KPa. Now we need to calculate the work related with the volume decreases as vapor exits the control volume or process 2-3 work boundary as:
. We can get from the saturated liquid chart the enthalpy he=hge=2675.5(KJ/Kg) @P=100KPa. Now we need to calculate the work related with the volume decreases as vapor exits the control volume or process 2-3 work boundary as:  . Now replacing every value in the time equation we get:
. Now replacing every value in the time equation we get: