Answer:
He probably tripped the wiring, when metal hits the electricity it creates a reaction that burns the wiring.
Explanation:
Answer:
Answer is attached.
Explanation:
A NMOS is a n-channel MOSFET or Metal Oxide
Semiconductor Field Effect Transistor. This type
of transistor might be an enhancement or
depletion type nMOS transistor designed using
layers of Metal-oxide, Silicon-oxide and Silicon
fabricated on a substrate.
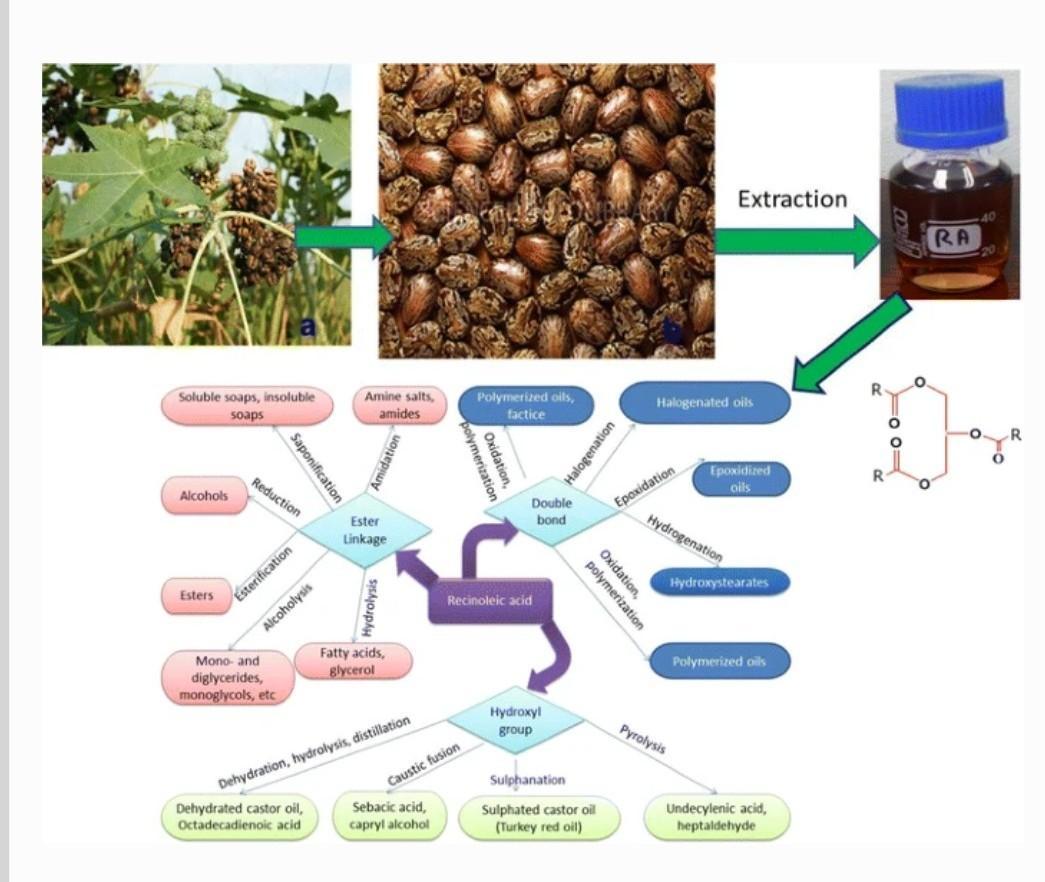
Castor oil is increasingly becoming an important bio-based raw material for industrial applications. The oil is non-edible and can be extracted from castor seeds from the castor plant belonging to the family Euphorbiaceae. The oil is a mixture of saturated and unsaturated fatty acid esters linked to a glycerol. The presence of hydroxyl group, a double bond, carboxylic group and a long chain hydrocarbon in ricinoleic acid (a major component of the oil), offer several possibilities of transforming it into variety of materials. The oil is thus a potential alternative to petroleum-based starting chemicals for the production of materials with variety of properties. Despite this huge potential, very little has recently been reviewed on the use of castor oil as a bio-resource in the production of functional materials. This review therefore highlights the potential of castor oil in the production of these diverse materials with their projected global market potential. The review gives the background information of castor oil and its geographical availability, the properties and its uses as bio-based resource for synthesis of various materials. The review further highlights on the use of castor oil or ricinoleic acid as a green capping agent in the synthesis of nanomaterials.
An ideal voltage source provides no energy when it is loaded by an open circuit (i.e. an infinite impedance), but approaches infinite energy and current when the load resistance approaches zero (a short circuit). ... An ideal current source has an infinite output impedance in parallel with the source.