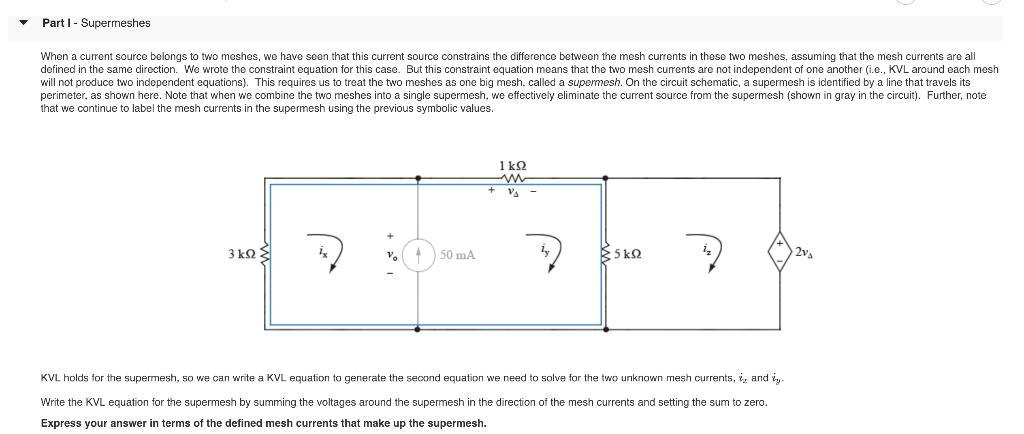
Answer:
C++ code is explained below
Explanation:
#include<iostream>
using namespace std;
//Function Declarations
void add();
void sub();
void mul();
//Main Code Displays Menu And Take User Input
int main()
{
int choice;
cout << "\nMenu";
cout << "\nChoice 1:addition";
cout << "\nChoice 2:subtraction";
cout << "\nChoice 3:multiplication";
cout << "\nChoice 0:exit";
cout << "\n\nEnter your choice: ";
cin >> choice;
cout << "\n";
switch(choice)
{
case 1: add();
break;
case 2: sub();
break;
case 3: mul();
break;
case 0: cout << "Exited";
exit(1);
default: cout << "Invalid";
}
main();
}
//Addition Of Matrix
void add()
{
int rows1,cols1,i,j,rows2,cols2;
cout << "\nmatrix1 # of rows: ";
cin >> rows1;
cout << "\nmatrix1 # of columns: ";
cin >> cols1;
int m1[rows1][cols1];
//Taking First Matrix
for(i=0;i<rows1;i++)
for(j=0;j<cols1;j++)
{
cout << "\nEnter element (" << i << "," << j << "): ";
cin >> m1[i][j];
cout << "\n";
}
//Printing 1st Matrix
for(i=0;i<rows1;i++)
{
for(j=0;j<cols1;j++)
cout << m1[i][j] << " ";
cout << "\n";
}
cout << "\nmatrix2 # of rows: ";
cin >> rows2;
cout << "\nmatrix2 # of columns: ";
cin >> cols2;
int m2[rows2][cols2];
//Taking Second Matrix
for(i=0;i<rows2;i++)
for(j=0;j<cols2;j++)
{
cout << "\nEnter element (" << i << "," << j << "): ";
cin >> m2[i][j];
cout << "\n";
}
//Displaying second Matrix
cout << "\n";
for(i=0;i<rows2;i++)
{
for(j=0;j<cols2;j++)
cout << m2[i][j] << " ";
cout << "\n";
}
//Displaying Sum of m1 & m2
if(rows1 == rows2 && cols1 == cols2)
{
cout << "\n";
for(i=0;i<rows1;i++)
{
for(j=0;j<cols1;j++)
cout << m1[i][j]+m2[i][j] << " ";
cout << "\n";
}
}
else
cout << "operation is not supported";
main();
}
void sub()
{
int rows1,cols1,i,j,k,rows2,cols2;
cout << "\nmatrix1 # of rows: ";
cin >> rows1;
cout << "\nmatrix1 # of columns: ";
cin >> cols1;
int m1[rows1][cols1];
for(i=0;i<rows1;i++)
for(j=0;j<cols1;j++)
{
cout << "\nEnter element (" << i << "," << j << "): ";
cin >> m1[i][j];
cout << "\n";
}
for(i=0;i<rows1;i++)
{
for(j=0;j<cols1;j++)
cout << m1[i][j] << " ";
cout << "\n";
}
cout << "\nmatrix2 # of rows: ";
cin >> rows2;
cout << "\nmatrix2 # of columns: ";
cin >> cols2;
int m2[rows2][cols2];
for(i=0;i<rows2;i++)
for(j=0;j<cols2;j++)
{
cout << "\nEnter element (" << i << "," << j << "): ";
cin >> m2[i][j];
cout << "\n";
}
for(i=0;i<rows2;i++)
{
for(j=0;j<cols2;j++)
cout << m1[i][j] << " ";
cout << "\n";
}
cout << "\n";
//Displaying Subtraction of m1 & m2
if(rows1 == rows2 && cols1 == cols2)
{
for(i=0;i<rows1;i++)
{
for(j=0;j<cols1;j++)
cout << m1[i][j]-m2[i][j] << " ";
cout << "\n";
}
}
else
cout << "operation is not supported";
main();
}
void mul()
{
int rows1,cols1,i,j,k,rows2,cols2,mul[10][10];
cout << "\nmatrix1 # of rows: ";
cin >> rows1;
cout << "\nmatrix1 # of columns: ";
cin >> cols1;
int m1[rows1][cols1];
for(i=0;i<rows1;i++)
for(j=0;j<cols1;j++)
{
cout << "\nEnter element (" << i << "," << j << "): ";
cin >> m1[i][j];
cout << "\n";
}
cout << "\n";
for(i=0;i<rows1;i++)
{
for(j=0;j<cols1;j++)
cout << m1[i][j] << " ";
cout << "\n";
}
cout << "\nmatrix2 # of rows: ";
cin >> rows2;
cout << "\nmatrix2 # of columns: ";
cin >> cols2;
int m2[rows2][cols2];
for(i=0;i<rows2;i++)
for(j=0;j<cols2;j++)
{
cout << "\nEnter element (" << i << "," << j << "): ";
cin >> m2[i][j];
cout << "\n";
}
cout << "\n";
//Displaying Matrix 2
for(i=0;i<rows2;i++)
{
for(j=0;j<cols2;j++)
cout << m2[i][j] << " ";
cout << "\n";
}
if(cols1!=rows2)
cout << "operation is not supported";
else
{
//Initializing results as 0
for(i = 0; i < rows1; ++i)
for(j = 0; j < cols2; ++j)
mul[i][j]=0;
// Multiplying matrix m1 and m2 and storing in array mul.
for(i = 0; i < rows1; i++)
for(j = 0; j < cols2; j++)
for(k = 0; k < cols1; k++)
mul[i][j] += m1[i][k] * m2[k][j];
// Displaying the result.
cout << "\n";
for(i = 0; i < rows1; ++i)
for(j = 0; j < cols2; ++j)
{
cout << " " << mul[i][j];
if(j == cols2-1)
cout << endl;
}
}
main();
}